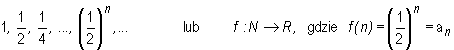
|
| następny punkt ≈ |
Podamy najpierw nieformalne, intuicyjne określenie ciągu. Jeśli ustalone liczby rzeczywiste ustawimy w pewnej określonej kolejności jedna za drugą, to powiemy, że jest to ciąg liczbowy lub krócej ciąg. Na przykład, jeśli ustawimy kolejno liczby parzyste uporządkowane rosnąco , to otrzymamy ciąg liczb parzystych: 2, 4, 6, 8, ..., 2(n + 1), ... . Podobnie, ciągiem liczb naturalnych nazwiemy uporządkowany rosnąco zbiór liczb naturalnych: 0, 1, 2, 3, 4, 5, .... , n, ... .
Zanim podamy ścisłą definicję ciągu liczbowego przypomnijmy definicję funkcji. Niech X, Y będą niepustymi zbiorami liczbowymi.
Definicja
Funkcją f określoną na zbiorze X o wartościach w zbiorze Y nazywamy przyporządkowanie każdej liczbie x ze zbioru X dokładnie jednej liczby f(x) ze zbioru Y.
Przyporządkowanie to możemy zapisać w różny sposób:
f : X
→ Y lub y = f(x), x ∈ X lub X ∍ x → f (x) ∈ Y.Jeśli zbiór X jest zbiorem liczb naturalnych N (lub jego podzbiorem postaci { n0, n0 + 1, ,,, }), to funkcję f nazywamy ciągiem liczbowym nieskończonym, lub krócej ciągiem. Zatem ciąg liczbowy jest szczególnym przypadkiem funkcji o wartościach rzeczywistych. Dla n ∈ N ( lub n ≥ n0 ), f(n) nazywamy n - tym wyrazem ciągu lub wyrazem ogólnym. W dalszej części wykładu symbolem N oznaczać będziemy zbiór indeksów, dla których określone są wyrazy rozważanych ciągów, a więc zbiór liczb naturalnych lub zbiór liczb naturalnych większych bądź równych od ustalonego n0.
Definicja
Jeśli każdej liczbie naturalnej n ∈ N przyporządkowana jest dokładnie jedna liczba rzeczywista an, to mówimy, że określony jest ciąg liczbowy (an).
Niektóre spotykane oznaczenia ciągu: (an) lub a0, a1,....., lub an, n = n0, n0+1, ..., lub {an}, (an)n∈N, (an, n ∈ N).
Liczbę an nazywamy wyrazem ogólnym ciągu lub n - tym elementem (wyrazem) ciągu. Często stosowane oznaczenia wyrazów ogólnych: an, bn, cn, xn, yn, ... .
Przykłady
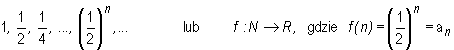
|
Powyżej, ciągi określane są poprzez podanie wzoru na wyraz ogólny. Można określać też ciągi opisowo, np. an = n-ta liczba pierwsza, (bn) = ciąg kwadratów liczb naturalnych, ciąg liczb pierwszych, ... .
Często, zwłaszcza w informatyce, ciągi definiowane są rekurencyjnie. Na przykład bezpośrednio określamy pierwszy wyraz ciągu jako ustaloną liczbę x0, a każdy kolejny wyraz xn+1 definiujemy przy pomocy poprzedniego xn: xn+1 = g(xn), gdzie g jest zadaną funkcją.
Przykłady
Pytanie kontrolne 1.1
Znajdź wyraz ogólny ciągu określonego rekurencyjnie:
x1
= 5, xn+1 = xn + 5, n = 1, 2, ... Zobacz odpowiedźGraficzną ilustracją ciągu jest jego wykres, tzn. zbiór punktów na płaszczyźnie
{ (n, an), n ∈ N }.
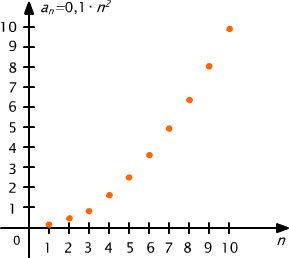
Rys. 1.1 Wykres ciągu o wyrazie ogólnym an = 0,1⋅ n2
Zbiór wyrazów ciągu { an , n ∈ N } przedstawimy graficznie jako podzbiór osi liczbowej.
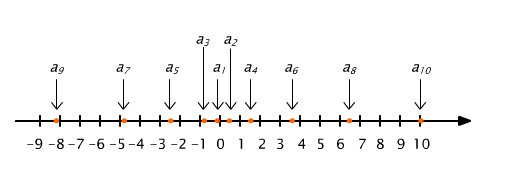
Rys. 1.2 Zbiór wartości ciągu o wyrazie ogólnym an = (− 1)n⋅ 0,1⋅ n2
Definicja
Mówimy, że ciąg (an) jest :
Przykłady
![]()
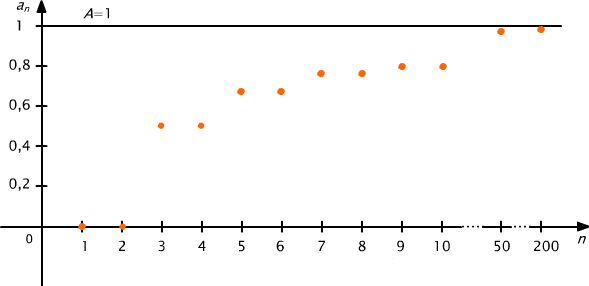
Rys. 1.3 Wykres ciągu niemalejącego i ograniczonego
Pytanie kontrolne 1.2
Czy ciąg o wyrazie ogólnym ![]() jest rosnący, ograniczony ?
jest rosnący, ograniczony ?
Ciąg niemalejący lub nierosnący nazywamy ciągiem monotonicznym, podczas gdy ciąg rosnący lub malejący nazywamy ciągiem ściśle monotonicznym. Zauważmy, że wprost z definicji wynika, że ciąg rosnący (malejący) jest również ciągiem niemalejącym (nierosnącym). Stąd też ciąg ściśle monotoniczny jest ciągiem monotonicznym.
Stwierdzenie
Ciąg (an) jest ograniczony ⇔ Ciąg (an) jest ograniczony z dołu i z góry.
Dowód
(konieczność: ⇒) Dla dowolnego n: ⎢ an ⎢ ≤ A ⇔ − A ≤ an ≤ A. Zatem ciąg jest ograniczony z dołu przez liczbę m = − A oraz z góry przez liczbę M = A.
(dostateczność: ⇐) Załóżmy, że − m ≤ an ≤ M. Przyjmując A = max {⎮ m⎮,⎮ M⎮ } otrzymujemy ⎢ an ⎢ ≤ A.
Definicja
Pytanie kontrolne 1.3
Znajdź wyraz ogólny ilorazu ciągów (an ), (bn ) takich, ż
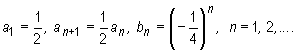
| następny punkt ≈ |