5. GRANICA NIEWŁAŚCIWA

Granica ciągu omawiana w poprzednich podpunktach jest czasem nazywana granicą właściwą, w odróżnieniu od granicy niewłaściwej. Istnieją dwie granice niewłaściwe: plus nieskończoność (lub krócej nieskończoność) oznaczana symbolem + ∞ (lub ∞) oraz minus nieskończoność oznaczana jako − ∞.

Definicja

Mówimy, że ciąg (a_n) jest rozbieżny do + ∞ , co zapisujemy symbolicznie

jeśli ( ∀ M ) ( ∃ δ ) ( ∀ n > δ ) a_n > M.

Ciąg rozbieżny do + ∞ to taki ciąg, którego wyrazy o dostatecznie dużych indeksach są dowolnie wielkie. Mówimy też, że ciąg (a_n) ma granicę niewłaściwą + ∞, lub krócej + ∞.

Pytanie kontrolne 1.11

Czy ciąg rozbieżny do + ∞ jest ograniczony z dołu?

Zobacz odpowiedź

Przykład

Niech M będzie dowolną liczbą. Są dwie możliwości

M < 0. Wówczas ( ∀ n ) n² > M
M > 0. Wówczas:

czyli (∀ n > δ ) n² > M, co należało wykazać.

Pytanie kontrolne 1.12

Wykaż, że ciąg (2ⁿ) jest rozbieżny do + ∞

Zobacz odpowiedź

Definicja

Mówimy, że ciąg (a_n) jest rozbieżny do − ∞, co zapisujemy symbolicznie

jeśli ( ∀ M ) ( ∃ δ ) ( ∀ n > δ ) a_n < M.

O ciągu rozbieżnym do − ∞ mówimy, że ma granicę niewłaściwą − ∞, lub krócej granicę − ∞. Jest on ograniczony z góry, nieograniczony z dołu.

Przykład

Ciąg ((− 2)ⁿ) jest nieograniczony, ale nie posiada granicy niewłaściwej. Dwa jego podciągi: ( − 2²ⁿ⁺¹) oraz (2²ⁿ) mają różne granice niewłaściwe: − ∞ oraz + ∞, odpowiednio. Zatem ma on wyrazy dowolnie duże oraz dowolnie małe. Nie może więc być zbieżny do granicy niewłaściwej.

Twierdzenie (o granicy niewłaściwej ciągu monotonicznego i nieograniczonego)

(i) Jeśli ciąg (a_n) jest niemalejący i nie jest ograniczony z góry, to

(ii) Jeśli ciąg (a_n) jest nierosnący i nie jest ograniczony z dołu, to

Z ostatniego twierdzenia wynika, że ciąg monotoniczny i nieograniczony ma granicę niewłaściwą. Zestawiając to twierdzenie z twierdzeniem o ciągu monotonicznym i ograniczonym widzimy, że każdy ciąg monotoniczny ma granicę - właściwą lub niewłaściwą, w zależności od tego, czy jest on ograniczony, czy tez nieograniczony.

Podamy teraz twierdzenia przydatne do obliczania granic. Nawiasy kwadratowe z symbolami ± ∞, wewnątrz są symbolicznymi zapisami granic ciągów określonego typu:

Twierdzenie

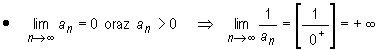
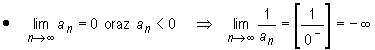
Przykłady

Ciąg o wyrazie ogólnym

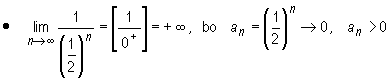
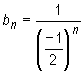
jest nieograniczony, ale nie posiada granicy niewłaściwej. Wprawdzie ciąg (( − 1 ⁄ 2 )ⁿ) jest zbieżny do zera, ale jego wyrazy o indeksach parzystych są dodatnie, natomiast wyrazy o indeksach nieparzystych są ujemne. Powoduje to, że podciąg ciągu (b_n) utworzony z wyrazów o indeksach parzystych ma granicę niewłaściwą + ∞ , a podciąg utworzony z wyrazów o indeksach nieparzystych ma granicę − ∞ . Zatem (b_n) ma wyrazy dowolnie duże oraz dowolnie małe. Nie może więc być zbieżny do granicy niewłaściwej.

Twierdzenie

Niech ciąg (a_n) ma granicę niewłaściwą, a ciąg (b_n) jest ograniczony lub ograniczony z dołu bądź z góry. Wówczas

Pytanie kontrolne 1.13

Czy posiada granicę ciąg o wyrazie ogólnym

Zobacz odpowiedź

Twierdzenie

Pytanie kontrolne 1.14

Czy posiada granicę ciąg o wyrazie ogólnym

Zobacz odpowiedź

Twierdzenie

Niech ciągi (a_n) i (b_n) mają odpowiednio granice a i b, które mogą być właściwe lub niewłaściwe. Wtedy granice ciągów ( a_n + b_n), ( a_nb_n ), oraz ciągu są symbolicznie przedstawione poniżej.

[+ ∞ + b ] = + ∞, gdy − ∞ < b ≤ + ∞

[− ∞ + b ] = − ∞, gdy − ∞ ≤ b < + ∞

[+ ∞ ⋅ b] = + ∞, gdy 0 < b ≤ + ∞

[+ ∞ ⋅ b] = − ∞, gdy − ∞ ≤ b < 0

[a^+∞ ] = 0, gdy 0 < a < 1

[a^+∞]= + ∞, gdy 1 < a ≤ + ∞

[(+ ∞ )^b]= 0, gdy − ∞ ≤ b < 0

[(+ ∞ )^b]= + ∞, gdy 0 < b ≤ + ∞

Przykłady

Pytanie kontrolne 1.15

Czy posiada granicę ciąg o wyrazie ogólnym

Zobacz odpowiedź

Wyrażenia nieoznaczone

Jeśli granice ciągów (a_n) i (b_n) są niewłaściwe lub mają wartość 0, to granice ciągów

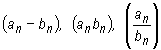
są nieoznaczone w poniżej symbolicznie opisanych przypadkach:

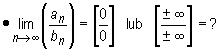
Oznacza to, że z góry nie można określić wartości tej granicy, tzn. może ona istnieć bądź też nie, może być granicą właściwą lub niewłaściwą, zależnie od konkretnych ciągów.

Przykłady

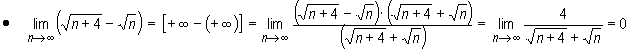
Pytanie kontrolne 1.16

Czy zbieżny jest ciąg o wyrazie ogólnym

Zobacz odpowiedź

Ponadto nieoznaczone są wyrażenia:

Twierdzenie (o dwóch ciągach)

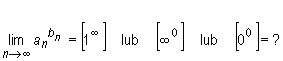
Niech (a_n), (b_n) będą takimi ciągami, że istnieje takie δ, że dla n ≥ δ mamy

a_n ≤ b_n. Wówczas

↔ poprzedni punkt następny punkt ≈