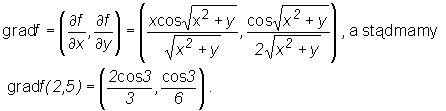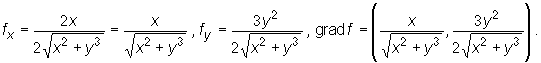1. GRADIENT
Definicja (gradient funkcji)
Niech f : D ⎯→
R, D ⊂
Rm, A∈
IntD. Jeżeli istnieją wszystkie pochodne cząstkowe 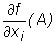 pierwszego rzędu funkcji f w punkcie A, to wektor
pierwszego rzędu funkcji f w punkcie A, to wektor 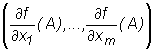 nazywamy gradientem funkcji f w punkcie A i oznaczamy gradf(A) lub ∇
f(A). Symbolem gradf (lub ∇
f) oznaczamy funkcję przyporządkowującą każdemu punktowi A w którym gradient jest określony, wektor gradf(A) czyli
nazywamy gradientem funkcji f w punkcie A i oznaczamy gradf(A) lub ∇
f(A). Symbolem gradf (lub ∇
f) oznaczamy funkcję przyporządkowującą każdemu punktowi A w którym gradient jest określony, wektor gradf(A) czyli 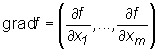 .
.
Przykład
•
Niech 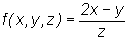 . Wyznaczymy grad f oraz grad f(0,1,3).
. Wyznaczymy grad f oraz grad f(0,1,3).
Mamy:
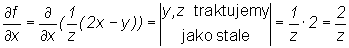 ,
,
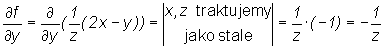 ,
,
 .
.
Zatem
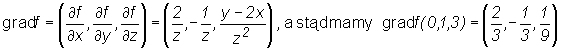 .
.
•
Wyznaczymy teraz gradf oraz gradf(2,5) dla funkcji 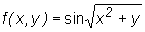 .
.
Mamy:
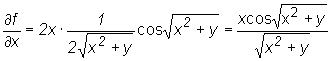 ,
,
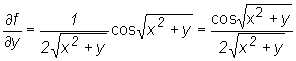 ,
,
zatem
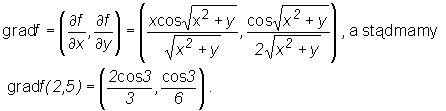
Następne twierdzenie i wniosek z niego pozwalają łatwo wyznaczać przybliżone wartości funkcji przy użyciu jej gradientu.
Twierdzenie
Niech f : D ⎯→
R, D ⊂
Rm . Jeśli funkcja f ma wszystkie pochodne cząstkowe pierwszego rzędu w punkcie A∈
IntD i pochodne te są ciągłe w punkcie A, to
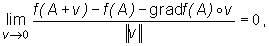
gdzie 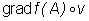 oznacza iloczyn skalarny tych wektorów, zaś
oznacza iloczyn skalarny tych wektorów, zaś 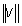 oznacza długość wektora v.
oznacza długość wektora v.
Wniosek
Jeśli funkcja f : D ⎯→
R, D ⊂
Rm ma w pewnym otoczeniu punktu A ciągłe pochodne cząstkowe pierwszego rzędu, to dla punktów X bliskich A mamy
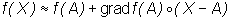 .
.
Niestety oszacowanie błędu tego przybliżenia przekracza ramy tego wykładu.
Przykład
Niech f(x,y) = xy. Obliczamy
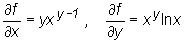 .
.
•
Dla A=(1,2), X =(1,02; 1,99) mamy
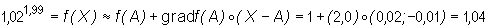
(z kalkulatora odczytujemy, że 1,021,99≈
1,04019...).
•
Dla A=(2,2), X =(1,98; 2,02) mamy
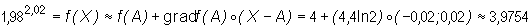
(z kalkulatora odczytujemy, że 1,982,02≈
3,9743...).
Przykład
Wyznaczymy gradient funkcji 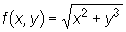 i stosując go obliczymy w przybliżeniu wartość wyrażenia
i stosując go obliczymy w przybliżeniu wartość wyrażenia 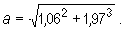
Mamy
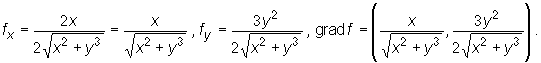
Ponadto a=f(X), gdzie X=(1,06; 1,97) oraz dla punktu A=(1;2) (bliskiego X) mamy f(A)=3. Zatem
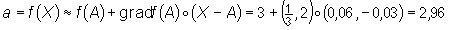
Interpretacja gradientu
- Wektor gradf(A) wskazuje kierunek najszybszego wzrostu wartości funkcji f w punkcie A. Wektor -gradf(A) wskazuje kierunek najszybszego spadku wartości funkcji f w punkcie A.
- Gdy f jest funkcją klasy C1 w zbiorze otwartym D ⊂
R2, K jest krzywą określoną równaniem f(x,y)=0, tj. K={(x,y)∈
D : f(x,y)=0} oraz gradf(A)≠
0 dla każdego punktu A∈
K,to w każdym punkcie (x0, y0)∈
K równanie stycznej do K w punkcie (x0,y0) jest postaci
gradf(x0,y0)°
(x-x0,y-y0) = 0.
Wektor gradf(x0,y0) nazywamy wektorem normalnym do krzywej K w punkcie (x0,y0).
- Gdy f jest funkcją klasy C1 w zbiorze otwartym D ⊂
R3, S jest powierzchnią określoną równaniem f(x,y,z)=0, tj. S={(x,y,z)∈
D : f(x,y,z)=0} oraz gradf(A)≠
0 dla każdego punktu A∈
S,to w każdym punkcie (x0,y0,z0)∈
S równanie płaszczyzny stycznej do S w punkcie (x0,y0,z0) jest postaci gradf(x0,y0,z0)°
(x-x0,y-y0,z-z0) = 0.
Wektor gradf(x0,y0,z0) nazywamy wektorem normalnym do powierzchni S w punkcie (x0,y0,z0).
Uzasadnimy jedynie punkt (1) (punkty (2) i (3) wymagają zbyt wiele rozważań geometrycznych).
Wielkość
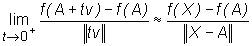 dla punktów X∈
D bliskich A oraz należących do półprostej {A+tv : t>0 } można uznać za miarę wzrostu wartości funkcji f w kierunku v.
dla punktów X∈
D bliskich A oraz należących do półprostej {A+tv : t>0 } można uznać za miarę wzrostu wartości funkcji f w kierunku v.
Tymczasem z poprzedniego twierdzenia łatwo wynika, że
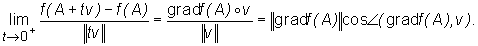
Zatem wielkość ta jest maksymalna, gdy wektory gradf(A) oraz v są równoległe i mają taki sam zwrot oraz jest minimalna, gdy wektory te są równoległe i mają przeciwny zwrot.
Przykład
•
Napiszmy równanie płaszczyzny stycznej w punkcie A=(2,2,2) do powierzchni S o równaniu
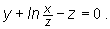
Mamy
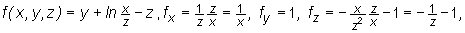
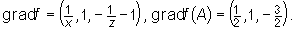
Zatem płaszczyzna styczna do powierzchni S w punkcie A=(2,2,2) ma równanie 
•
Wyznaczmy równanie płaszczyzny stycznej w punkcie A=(1,-1,4) do powierzchni S o równaniu
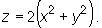
Przepisujemy równanie powierzchni w postaci f(x,y,z)=0, gdzie
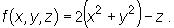
Mamy
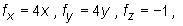
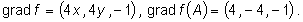
Zatem płaszczyzna styczna do powierzchni S w punkcie A=(1,-1,4) ma równanie
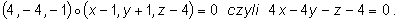
•
Napisz równanie prostej stycznej w punkcie A=(2,-1) do krzywej K o równaniu
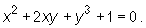
Mamy
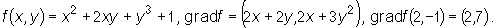
Zatem prosta styczna do krzywej K w punkcie A=(2,-1) ma równanie 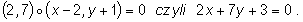
![]() pierwszego rzędu funkcji f w punkcie A, to wektor
pierwszego rzędu funkcji f w punkcie A, to wektor 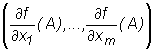 nazywamy gradientem funkcji f w punkcie A i oznaczamy gradf(A) lub ∇
f(A). Symbolem gradf (lub ∇
f) oznaczamy funkcję przyporządkowującą każdemu punktowi A w którym gradient jest określony, wektor gradf(A) czyli
nazywamy gradientem funkcji f w punkcie A i oznaczamy gradf(A) lub ∇
f(A). Symbolem gradf (lub ∇
f) oznaczamy funkcję przyporządkowującą każdemu punktowi A w którym gradient jest określony, wektor gradf(A) czyli 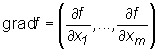 .
.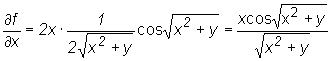 ,
,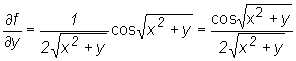 ,
,