3. RÓŻNICZKOWANIE FUNKCJI ZŁOŻONEJ
W paragrafie tym podajemy kilka twierdzeń dotyczących pochodnych funkcji złożonych w przypadku gdy co najmniej jedna ze składanych funkcji jest funkcją wielu zmiennych.
Zasadniczym twierdzeniem z którego wynikają wszystkie pozostałe twierdzenia tego paragrafu jest następujące:
Twierdzenie (o pochodnych cząstkowych funkcji złożonej)
Załóżmy, że
- funkcje x1(u1,...,un),..., xm(u1,u2,...,un) mają pochodne cząstkowe pierwszego rzędu w pewnym otoczeniu punktu A ciągłe w punkcie A;
- funkcja f(x1,x2,...,xm) ma pochodne cząstkowe pierwszego rzędu w pewnym otoczeniu punktu X= (x1(A), ..., xm(A)), ciągłe w punkcie X.
Wówczas funkcja złożona F(u1,...,un) = f(x1(u1,...,un), ..., xm(u1,...,un)) ma pochodne cząstkowe pierwszego rzędu w punkcie A oraz
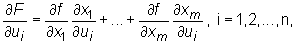
gdzie pochodne 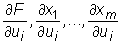 są liczone w punkcie A, zaś pochodne
są liczone w punkcie A, zaś pochodne 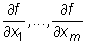 w punkcie X = (x1(A),...,xm(A)).
w punkcie X = (x1(A),...,xm(A)).
Powyższe wzory można zapisać w postaci iloczynu macierzy
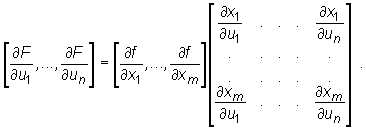
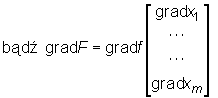
Uwaga
Gdy m=n=1 to wzór z powyższego twierdzenia przybiera postać
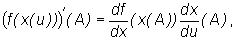
czyli jest po prostu wzorem na pochodną funkcji złożonej jednej zmiennej.
Dla m = 1 ostatnie twierdzenie przybiera postać:
Twierdzenie
Jeśli
- funkcja x(u1,...,un) ma pochodne cząstkowe pierwszego rzędu w pewnym otoczeniu punktu A ciągłe w punkcie A
- funkcja f(x) jednej zmiennej ma pochodną właściwą w pewnym otoczeniu punktu x0=x(A)
to funkcja złożona F(u1,...,un) = f(x(u1,...,un)) ma pochodne cząstkowe pierwszego rzędu w punkcie A oraz
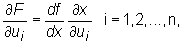
gdzie pochodne 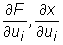 są liczone w punkcie A, zaś pochodna
są liczone w punkcie A, zaś pochodna 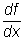 w punkcie x0=x(A).
w punkcie x0=x(A).
Powyższy wzór można zapisać w postaci iloczynu macierzy
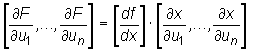
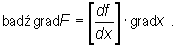
Gdy n = 1 to twierdzenie o pochodnych cząstkowych funkcji złożonej przybiera postać:
Twierdzenie
Jeśli
- funkcje x1=x1(t), ...,xm=xm(t) mają pochodne właściwe w punkcie t0
- funkcja f(x1,...,xm) ma pochodne cząstkowe pierwszego rzędu w pewnym otoczeniu punktu X0=f(x1(t0),...,xm(t0))
to funkcja złożona F(t) = f(x1(t), ..., xm(t)) ma pochodną właściwą w punkcie t0 oraz 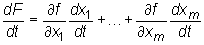 , gdzie pochodne
, gdzie pochodne 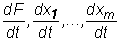 są liczone w punkcie t0, zaś pochodne
są liczone w punkcie t0, zaś pochodne 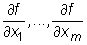 w punkcie X0.
w punkcie X0.
Uwaga: W poniższych przykładach dla prostoty zapisu przyjęto nieco inne oznaczenia argumentów funkcji.
Przykłady
•
Obliczmy 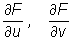 , gdy F(u,v)=e2xcosy, gdzie x = u2 - v2, y=2uv.
, gdy F(u,v)=e2xcosy, gdzie x = u2 - v2, y=2uv.
Mamy F(u,v) = f(x(u,v), y(u,v)), gdzie f(x,y)=e2xcosy.
Ponieważ
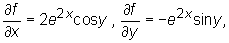
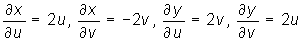
oraz 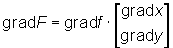
czyli
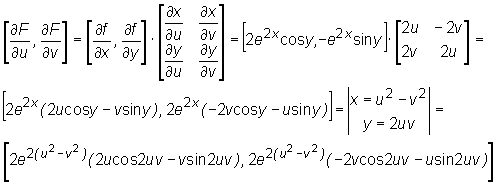
Zatem
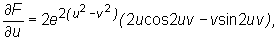
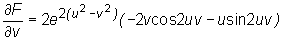 .
.
•
Niech 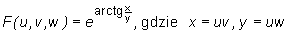 . Obliczmy
. Obliczmy 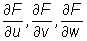 .
.
Mamy: F(u,v,w) = f(x(u,v,w), y(u,v,w)), gdzie f(x,y)=earctg(x/y).
Ponieważ
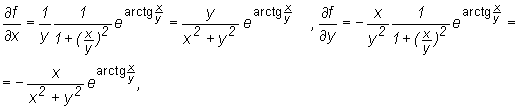
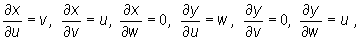
to 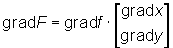
czyli
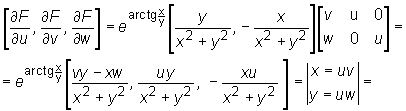
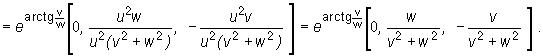
Zatem
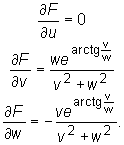
•
Obliczmy 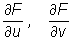 , gdy F(u,v)=f(x,y,z), gdzie x = uv, y=u+v, z=u/v, zaś o funkcji f wiemy tyle, że ma ona ciągłe pochodne cząstkowe pierwszego rzędu.
, gdy F(u,v)=f(x,y,z), gdzie x = uv, y=u+v, z=u/v, zaś o funkcji f wiemy tyle, że ma ona ciągłe pochodne cząstkowe pierwszego rzędu.
Mamy 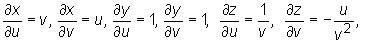
oraz 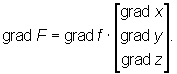 Stąd
Stąd
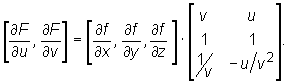 Oznacza to, że
Oznacza to, że
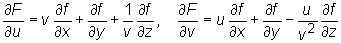 .
.
W powyższych wzorach pochodne cząstkowe 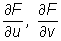 są liczone w punkcie (u, v) zaś pochodne cząstkowe
są liczone w punkcie (u, v) zaś pochodne cząstkowe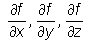 w punkcie (uv, u+v,u/v).
w punkcie (uv, u+v,u/v).
•
Obliczmy 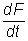 , gdy
, gdy 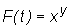 , gdzie x=lnt, y=sint.
, gdzie x=lnt, y=sint.
Mamy F(t)=f(x(t),y(t)), gdzie f(x,y)=xy. Ponadto
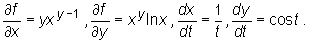
Zatem
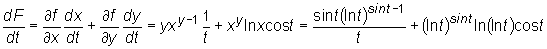
•
Obliczmy 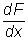 , gdy
, gdy 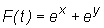 , gdzie
, gdzie 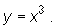
Mamy F(x)=f(x,y(x)), gdzie 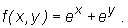 Ponadto
Ponadto
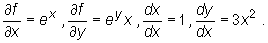
Zatem
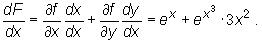
![]()
![]() są liczone w punkcie A, zaś pochodne
są liczone w punkcie A, zaś pochodne ![]() w punkcie X = (x1(A),...,xm(A)).
w punkcie X = (x1(A),...,xm(A)).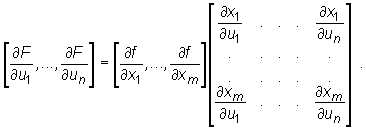
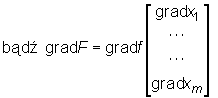
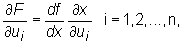
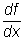 w punkcie x0=x(A).
w punkcie x0=x(A).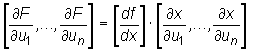
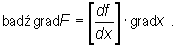
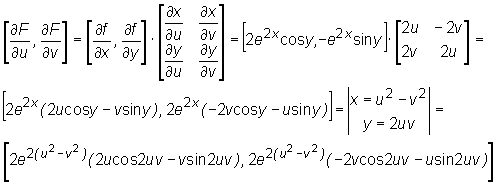
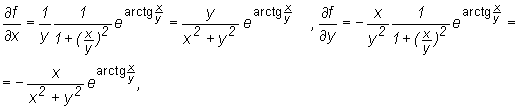
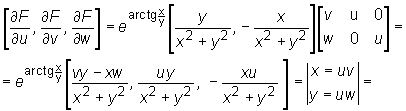
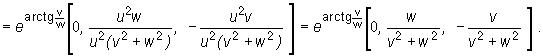
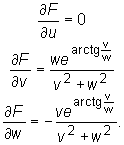
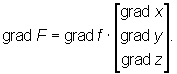 Stąd
Stąd 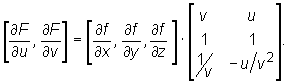 Oznacza to, że
Oznacza to, że