Definicja (punkt stacjonarny)
Niech f : D→ R, (D⊂ Rm). Mówimy, że punkt A ∈ D jest punktem stacjonarnym funkcji f jeśli
| ↔ poprzedni punkt |
Definicja (maksimum lokalne funkcji w punkcie)
Mówimy, że funkcja f : D→ R, (D⊂ Rm) ma w punkcie A∈ D
Zmieniając w powyższych definicjach znaki nierówności na przeciwne otrzymujemy definicję minimum lokalnego oraz właściwego minimum lokalnego.
Gdy funkcja f ma w punkcie A maksimum lokalne lub minimum lokalne to mówimy, że f ma w A ekstremum lokalne.
Definicja (punkt stacjonarny)
Niech f : D→ R, (D⊂ Rm). Mówimy, że punkt A ∈ D jest punktem stacjonarnym funkcji f jeśli
Twierdzenie (warunek konieczny istnienia ekstremum lokalnego)
Niech f : D→ R, (D⊂ Rm) oraz A ∈ D. Wówczas jeśli
a) f ma ekstremum lokalne w punkcie A
b) istnieją pochodne cząstkowe 
to A jest punktem stacjonarnym funkcji f.
Wniosek
Funkcja 
może mieć ekstrema lokalne tylko w punktach stacjonarnych lub w punktach w których nie istnieje co najmniej jedna z jej pochodnych cząstkowych pierwszego rzędu. W dalszym ciągu będziemy się zajmować tylko funkcjami, które w każdym punkcie swojej dziedziny mają wszystkie pochodne cząstkowe pierwszego rzędu, a zatem mogą mieć ekstrema lokalne tylko w punktach stacjonarnych.
Uwaga
Warunek stacjonarności jest tylko warunkiem koniecznym istnienia ekstremum lokalnego, nie jest natomiast warunkiem wystarczającym.
Na przykład punkt (0,0) jest jedynym punktem stacjonarnym funkcji 
ale funkcja ta nie ma ekstremum lokalnego w punkcie A=(0,0). Fakt, że funkcja ta nie ma w punkcie (0,0) ekstremum lokalnego wynika to z tego, że dla dowolnego r > 0 mamy (r/2,0) ∈
O(A, r) oraz (0,r/2)∈
O(A, r) przy czym f(0,r/2) < f(A)=0 < f(r/2,0).
Uwaga
Jeśli funkcja 2 zmiennych z=f(x,y) ma w punkcie wszystkie pochodne cząstkowe drugiego rzędu to wyznacznik
będziemy oznaczać krótko W(A).
Twierdzenie (warunek wystarczający istnienia ekstremum lokalnego funkcji dwóch zmiennych)
Niech 
będzie punktem stacjonarnym funkcji z=f(x,y). Ponadto niech funkcja f ma w pewnym otoczeniu punktu A ciągłe wszystkie pochodne cząstkowe drugiego rzędu. Wówczas:
Uwaga
Jeśli A jest punktem stacjonarnym funkcji z=f(x,y) oraz
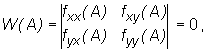
to funkcja f może zarówno mieć jak i nie mieć ekstremum lokalnego w punkcie A. W takim przypadku praktycznie jedyną metodą zbadania czy f ma w A ekstremum lokalne jest skorzystanie z definicji.
Przykłady
Wyznaczymy wszystkie ekstrema lokalne następujących funkcji dwóch zmiennych:
•
Wyznaczamy pochodne cząstkowe pierwszego rzędu funkcji f :
Wyznaczamy punkty stacjonarne funkcji f rozwiązując układ równań
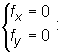
Jest tylko jeden punkt stacjonarny A = (1,0).
Wyznaczamy pochodne cząstkowe drugiego rzędu funkcji f :
Ponieważ
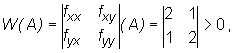
to funkcja f ma w punkcie A ekstremum lokalne. Z tego, że 
wynika, że f ma w punkcie A minimum lokalne.
•
Wyznaczamy pochodne cząstkowe pierwszego rzędu funkcji f :
Wyznaczamy punkty stacjonarne funkcji f rozwiązując układ równań
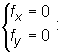
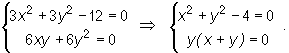
Zauważmy, że
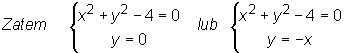
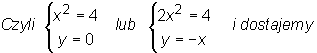
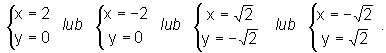
Są 4 punkty stacjonarne :
Wyznaczamy pochodne cząstkowe drugiego rzędu funkcji f :
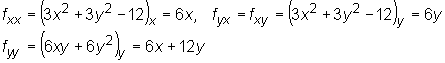
Zatem
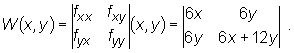
Wyznaczamy wartości wyznacznika W(x,y) w punktach stacjonarnych i badamy charakter tych punktów:
•
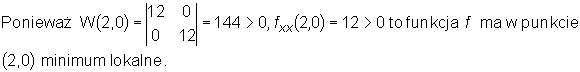
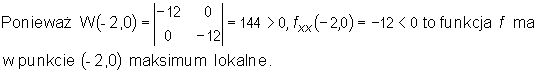
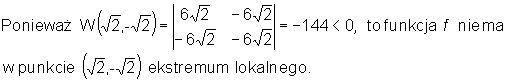
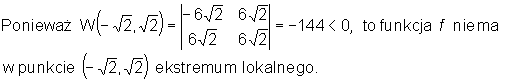
Mamy
Wyznaczamy punkty stacjonarne funkcji f rozwiązując układ równań
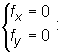
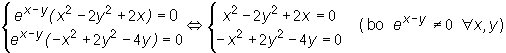
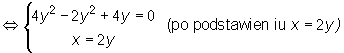
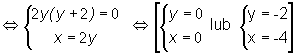
Są 2 punkty stacjonarne :
Wyznaczamy pochodne cząstkowe drugiego rzędu funkcji f :
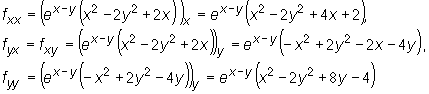
Zatem
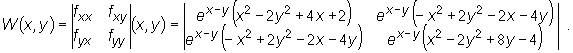
Wyznaczamy wartości wyznacznika W(x,y) w punktach stacjonarnych i badamy charakter tych punktów:
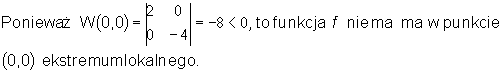
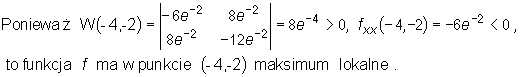
| ↔ poprzedni punkt |