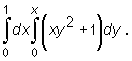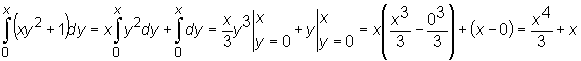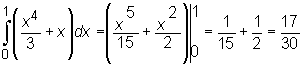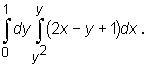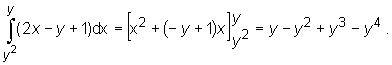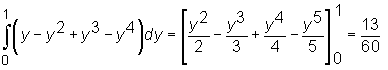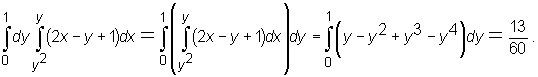1. DWUKROTNE CAŁKI ITEROWANE
Definicja (obszar normalny względem osi Ox)
Obszarem normalnym względem osi Ox nazywamy obszar D⊂
R2 postaci D=
{(x,y) : a ≤
x ≤
b , p(x) ≤
y ≤
q(x)}, gdzie a <
b, zaś p(x) i q(x) są ciągłymi funkcjami określonymi na przedziale [a, b] takimi, że p(x) ≤
q(x) dla każdego x∈
[a,b].
Analogicznie definiujemy obszar normalny względem osi Oy:
Definicja (obszar normalny względem osi Oy)
Obszarem normalnym względem osi Oy nazywamy obszar D⊂
R2 postaci
D =
{(
x,y):
c ≤
y ≤
d, r(
y)
≤
x ≤
s (
y)} gdzie
a <
b, zaś
r(y) i
s(y) są ciągłymi funkcjami określonymi na przedziale
[c,d] takimi, że
r(
y)
≤
s(
y) dla każdego
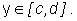
Uwaga
Intuicyjnie, domknięty i ograniczony obszar D jest normalny względem osi Ox jeśli każda prosta prostopadła do osi Ox przecinająca D przecina go wzdłuż odcinka (być może jednopunktowego). Zbiór górnych końców takich odcinków nazywamy górnym brzegiem obszaru D, natomiast zbiór dolnych końców takich odcinków dolnym brzegiem obszaru D.
Jeśli obszar D jest normalny względem osi Ox to
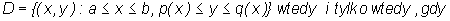
•
rzutem zbioru D na oś Ox jest odcinek [a,b]
•
dolny brzeg obszaru D jest krzywą o równaniu y=p(x)
•
górny brzeg obszaru D jest krzywą o równaniu y=q(x).
Podobnie domknięty i ograniczony i obszar D jest normalny względem osi Oy jeśli każda prosta prostopadła do osi Oy przecinająca D przecina go wzdłuż odcinka (być może jednopunktowego). Zbiór lewych końców takich odcinków nazywamy lewym brzegiem obszaru D, natomiast zbiór prawych końców takich odcinków prawym brzegiem obszaru D.
Jeśli obszar D jest normalny względem osi Oy to
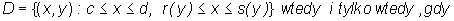
•
rzutem zbioru D na oś Oy jest odcinek [c,d]
•
lewy brzeg obszaru D jest krzywą o równaniu x=r(y)
•
prawy brzeg obszaru D jest krzywą o równaniu x=s(y).
Przykłady
•
Obszar D1 jest obszarem normalnym względem osi Ox, ale nie jest normalny względem osi Oy
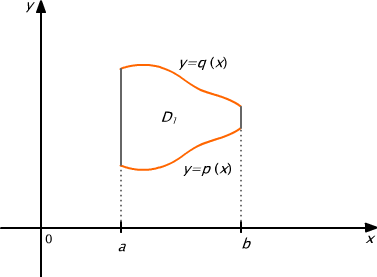
Rys. 15.1
•
Obszar D2 jest obszarem normalnym względem osi Oy, ale nie jest normalny względem osi Ox
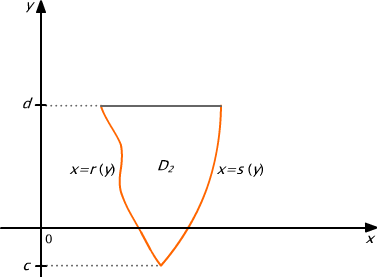
Rys. 15.2
•
Obszar D3 jest obszarem normalnym zarówno względem osi Ox, jak i osi Oy
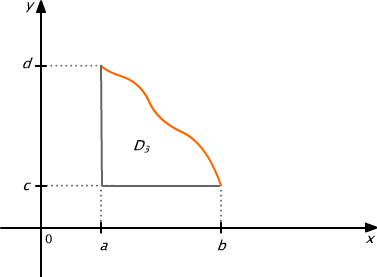
Rys. 15.3
•
Obszar D4 nie jest obszarem normalnym ani względem osi Ox, ani względem osi Oy
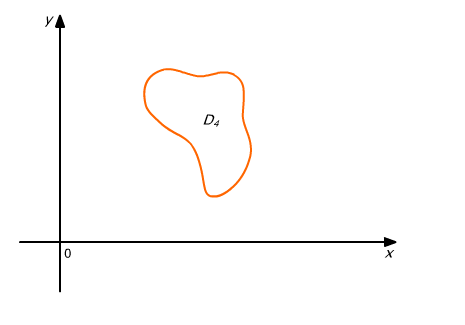
Rys. 15.4
Definicja (dwukrotna całka iterowana)
Niech funkcja f będzie ciągła na obszarze D =
{(x,y) : a ≤
x ≤
b, p(x) ≤
y ≤
q(x)} normalnym względem osi Ox (z definicji obszaru normalnego względem osi Ox wynika, że funkcje p(x), q(x) są ciągłe na przedziale [a, b]).
Ustalamy element x∈
[a,b] i traktujemy funkcję f(x,y) jako funkcję argumentu y określoną na przedziale [p(x),q(x)]. Otrzymana w ten sposób funkcja zmiennej y (na ogół inna dla każdego x) jest ciągła w przedziale [p(x),q(x)], a zatem ma ona skończoną całkę Riemanna na tym przedziale oznaczaną
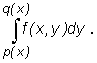
Można udowodnić, że funkcja A(x) zmiennej x określona wzorem
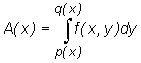
jest ciągła na przedziale [a,b], a zatem ma ona na nim skończoną całkę Riemanna
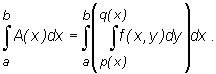
Podobnie, jeśli funkcja f jest ciągła na obszarze D =
{(x,y) : c ≤
y ≤
d, r(y) ≤
x ≤
s(y)} normalnym względem osi Oy, to traktując zmienną y jako stałą możemy obliczyć całkę funkcji f(x,y) traktowanej jako funkcja zmiennej x w przedziale [r(y),s(y)] oznaczaną
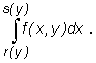
Otrzymana w ten sposób funkcja B(y) zmiennej y określona wzorem
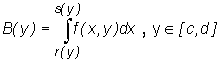
jest ciągła na przedziale [c,d], a zatem istnieje jej całka Riemanna na tym przedziale
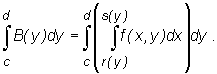
Otrzymane w ten sposób całki
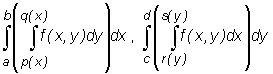
nazywamy (dwukrotnymi) całkami iterowanymi funkcji f.
Całkę 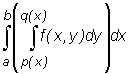 oznacza się na ogół
oznacza się na ogół 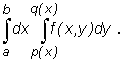
W przypadku tej całki iterowanej całkę 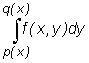 nazywamy całką wewnętrzną, zaś całkę
nazywamy całką wewnętrzną, zaś całkę 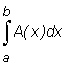 (gdzie
(gdzie 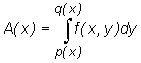 ) całką zewnętrzną.
) całką zewnętrzną.
Całkę 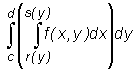 oznacza się na ogół
oznacza się na ogół 
W przypadku tej całki iterowanej całkę 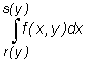 nazywamy całką wewnętrzną, zaś całkę
nazywamy całką wewnętrzną, zaś całkę 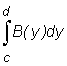 (gdzie
(gdzie 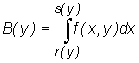 ) całką zewnętrzną.
) całką zewnętrzną.
Przykład
Obliczmy całkę iterowaną 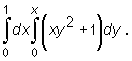
Najpierw obliczamy całkę wewnętrzną całkując względem y i traktując zmienną x jako stałą :
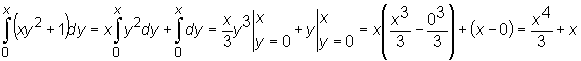
Następnie obliczamy całkę zewnętrzną (z otrzymanej w wyniku pierwszego całkowania funkcji zmiennej x):
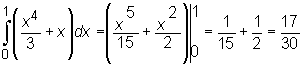
otrzymując ostatecznie:

Przykład
Obliczmy całkę iterowaną 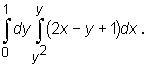
Najpierw obliczamy całkę wewnętrzną całkując względem x i traktując y jako stałą:
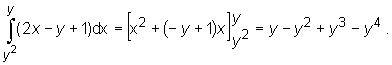
Następnie obliczamy całkę zewnętrzną (z otrzymanej w wyniku pierwszego całkowania funkcji zmiennej y):
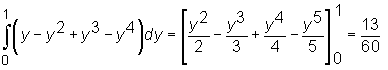
otrzymując ostatecznie:
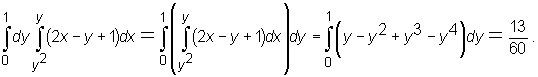




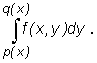
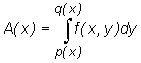
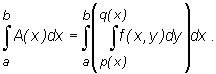
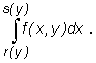
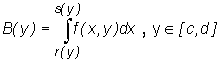
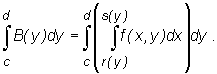
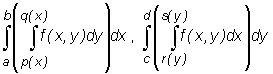
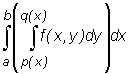 oznacza się na ogół
oznacza się na ogół 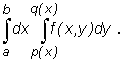
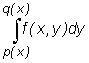 nazywamy całką wewnętrzną, zaś całkę
nazywamy całką wewnętrzną, zaś całkę 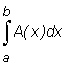 (gdzie
(gdzie 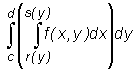 oznacza się na ogół
oznacza się na ogół 
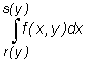 nazywamy całką wewnętrzną, zaś całkę
nazywamy całką wewnętrzną, zaś całkę 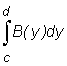 (gdzie
(gdzie 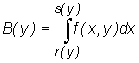 ) całką zewnętrzną.
) całką zewnętrzną.