| ↔ poprzedni punkt | następny punkt ≈ |
Załóżmy, że funkcja f : P → R jest funkcją określoną na prostokącie P = { (x, y) ∈ R2 : a ≤ x≤ b, c ≤ y ≤ d } o bokach równoległych do osi układu współrzędnych.
Przez podział prostokąta P rozumiemy dowolny ciąg Pn = (P1, P2,..., Pn) prostokątów o bokach równoległych do osi układu współrzędnych i o parami rozłącznych wnętrzach taki, że ![]()
Niech D xi, D yi oznaczają długości boków prostokąta Pi, zaś ⎢ Pi⎥ niech oznacza pole tego prostokąta czyli ⎢ Pi⎥ =D xi ⋅ D yi.
Średnicą podziału P n nazywamy długość dn najdłuższej z przekątnych prostokątów P1, P2,..., Pn.
W każdym prostokącie Pi wybieramy po jednym punkcie Ai=
(xi, yi) i wyznaczamy sumę ![]() nazywaną sumą całkową (Riemanna) funkcji f po prostokącie P, odpowiadającą podziałowi Pn =(P1,P2,...,Pn) oraz wyborowi punktów pośrednich (A1,A2,...,An).
nazywaną sumą całkową (Riemanna) funkcji f po prostokącie P, odpowiadającą podziałowi Pn =(P1,P2,...,Pn) oraz wyborowi punktów pośrednich (A1,A2,...,An).
Normalnym ciągiem podziałów nazywamy ciąg 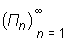 podziałów, których średnice tworzą ciąg zbieżny do zera, zaś ciąg sum całkowych odpowiadający normalnemu ciągowi podziałów (przy dowolnym wyborze punktów Ai) nazywamy normalnym ciągiem sum całkowych funkcji f po prostokącie P.
podziałów, których średnice tworzą ciąg zbieżny do zera, zaś ciąg sum całkowych odpowiadający normalnemu ciągowi podziałów (przy dowolnym wyborze punktów Ai) nazywamy normalnym ciągiem sum całkowych funkcji f po prostokącie P.
Definicja (całka podwójna po prostokącie)
Niech f będzie funkcją rzeczywistą określoną na prostokącie P⊂ R2.
Powiemy, że funkcja f jest całkowalna (w sensie Riemanna) na prostokącie P, jeśli istnieje liczba rzeczywista s taka, że każdy normalny ciąg sum całkowych funkcji f po prostokącie P jest zbieżny do s.
Liczbę s nazywamy całką podwójną (Riemanna) funkcji f po prostokącie P i oznaczamy ją symbolem ![]() .
.
Podkreślmy, że granica s ma być taka sama dla wszystkich normalnych ciągów podziałów prostokąta P i wszystkich możliwych wyborów ciągów punktów pośrednich.
Definicja (całka podwójna po obszarze)
Niech f będzie funkcją rzeczywistą określoną na domkniętym ograniczonym obszarze D⊂ R2 oraz niech P będzie dowolnym prostokątem o bokach równoległych do osi układu współrzędnych zawierającym D. Na prostokącie P określamy funkcję f∗ w następujący sposób:
![]() .
.
Jeżeli istnieje całka podwójna funkcji f∗
po prostokącie P, to mówimy, że funkcja f jest całkowalna na obszarze D, zaś liczbę ![]() nazywamy całką podwójną (Riemanna) funkcji f po obszarze D i oznaczamy symbolem
nazywamy całką podwójną (Riemanna) funkcji f po obszarze D i oznaczamy symbolem ![]() lub
lub ![]()
Uwaga
Można wykazać, że istnienie i wielkość liczby ![]() nie zależą od wyboru prostokąta P zawierającego obszar D.
nie zależą od wyboru prostokąta P zawierającego obszar D.
Twierdzenie (własności całki podwójnej)
Niech D⊂ R2 będzie obszarem domkniętym i ograniczonym oraz niech f i g będą funkcjami rzeczywistymi określonymi na D i całkowalnymi na tym obszarze. Wtedy
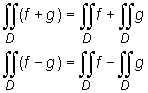
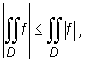
Warunek wystarczający istnienia całki podwójnej funkcji f po obszarze D i sposób jej obliczania podaje następujące:
Twierdzenie
Jeżeli obszar D = {(x, y) : a ≤ x ≤ b, p(x) ≤ y ≤ q(x)} jest obszarem normalnym względem osi Ox , to każda funkcja f ciągła na obszarze D jest na tym obszarze całkowalna. Ponadto zachodzi równość
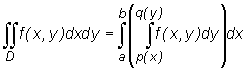
Prawa strona tego wzoru jest także zapisywana bez użycia nawiasów:
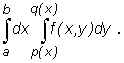
Oznacza to, że obliczenie całki podwójnej sprowadza się w tym przypadku do obliczenia pewnej dwukrotnej całki iterowanej.
Analogiczne twierdzenie jest prawdziwe dla obszarów normalnych względem osi Oy :
Twierdzenie
Jeżeli obszar D = {(x, y): c ≤ y ≤ d, r(y) ≤ x ≤ s(y)} jest obszarem normalnym względem osi Oy , to każda funkcja f ciągła na obszarze D jest na tym obszarze całkowalna. Ponadto zachodzi równość
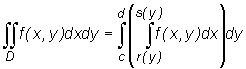
Prawa strona tego wzoru jest także zapisywana bez użycia nawiasów:
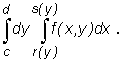
Przykład
Obliczmy całkę 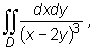 gdzie
gdzie ![]() jest prostokątem o bokach równoległych do osi układu współrzędnych (por. Rys. 15.5).
jest prostokątem o bokach równoległych do osi układu współrzędnych (por. Rys. 15.5).
Rys. 15.5
Obszar D jest normalny względem obu osi. Traktując D jako obszar normalny względem osi Ox otrzymujemy zamianę całki podwójnej na całkę iterowaną:
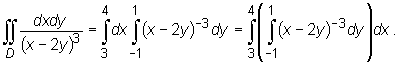
Najpierw obliczmy całkę nieoznaczoną ![]()
Traktując x jako stałą otrzymujemy
![]()
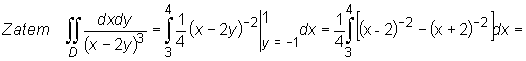
![]()
Traktując D jako obszar normalny względem osi Oy otrzymujemy następującą zamianę całki podwójnej na całkę iterowaną: 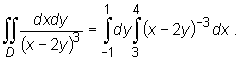
Czytelnik zechce sprawdzić, że po obliczeniu tej całki iterowanej ponownie otrzymujemy liczbę 7/60.
Przykład
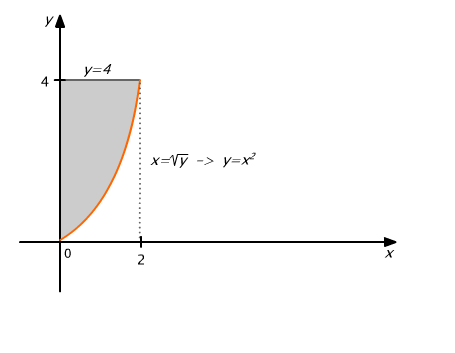
Obliczmy całkę ![]() gdzie D jest obszarem ograniczonym łukami krzywych
gdzie D jest obszarem ograniczonym łukami krzywych ![]() (por. Rys. 15.6)
(por. Rys. 15.6)

Rys. 15.6
Obszar D jest normalny zarówno względem osi Ox , jak i osi Oy .
Najpierw obliczmy całkę traktując D jako obszar normalny względem osi Ox .
Rzutem zbioru D na oś Ox jest odcinek [0,2]. Górny brzeg zbioru D ma równanie ![]() , a dolny brzeg ma równanie
, a dolny brzeg ma równanie ![]()
Zatem ![]() Stąd otrzymujemy zamianę całki podwójnej na całkę iterowaną:
Stąd otrzymujemy zamianę całki podwójnej na całkę iterowaną:
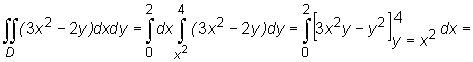
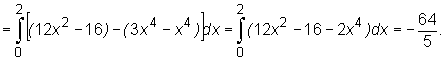
Obliczmy teraz całkę traktując D jako obszar normalny względem osi Oy .
Rzutem zbioru D na oś Oy jest odcinek [0,4]. Lewy brzeg zbioru D ma równanie ![]() , a prawy - równanie
, a prawy - równanie ![]()
Zatem ![]() Stąd otrzymujemy zamianę całki podwójnej na całkę iterowaną:
Stąd otrzymujemy zamianę całki podwójnej na całkę iterowaną:
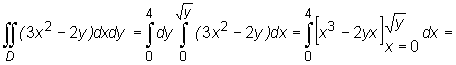
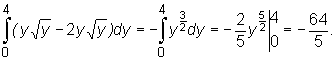
Uwaga
Oczywiście, gdy obszar jest normalny względem obu osi, to wystarczy zamienić całkę podwójną w jeden sposób na całkę iterowaną i obliczyć ją. Wynika to z tego, że całkując w odwrotnej kolejności otrzymamy ten sam wynik po innych rachunkach. Czasem zdarza się, że stosując jeden z tych sposobów otrzymujemy dużo trudniejsze całki nieoznaczone (np. całki nie wyrażające się przez funkcje elementarne) niż stosując drugi z tych sposobów.
Przykład
Obliczmy całkę ![]() gdzie D jest obszarem ograniczonym odcinkami prostych
gdzie D jest obszarem ograniczonym odcinkami prostych ![]() (por. Rys. 15.7)
(por. Rys. 15.7)
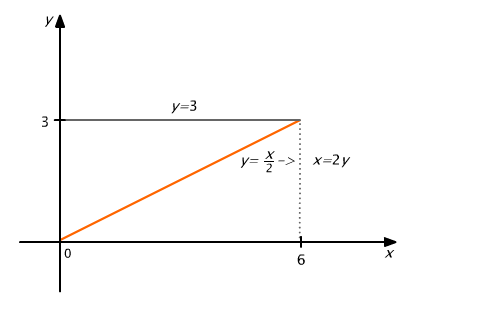
Rys. 15.7
Obszar D jest normalny względem obu osi. Rzutem zbioru D na oś Ox jest odcinek [0,6]. Górny brzeg zbioru D ma równanie ![]() , a dolny brzeg ma równanie
, a dolny brzeg ma równanie ![]()
Zatem ![]() i traktując D jako obszar normalny względem osi Ox dostajemy:
i traktując D jako obszar normalny względem osi Ox dostajemy:
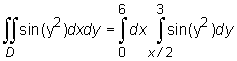
i pojawia się "drobny" kłopot - całka nieoznaczona ![]() nie wyraża się przez funkcje elementarne tj. nie ma żadnej funkcji elementarnej f takiej, że
nie wyraża się przez funkcje elementarne tj. nie ma żadnej funkcji elementarnej f takiej, że ![]()
Zatem próbujemy obliczyć całkę podwójną traktując D jako obszar normalny względem osi Oy .
Rzutem zbioru D na oś Oy jest odcinek [0,3]. Lewy brzeg zbioru D ma równanie ![]() , a prawy - równanie
, a prawy - równanie ![]()
Zatem ![]() Stąd
Stąd
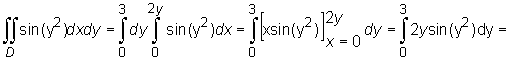
![]()
Skorzystaliśmy z tego, że

Przykład
Obliczmy całkę ![]() gdzie D jest obszarem ograniczonym łukami krzywych y=sinx x∈
[0,π
], y=3sinx x∈
[0,π
] (por. Rys. 15.8)
gdzie D jest obszarem ograniczonym łukami krzywych y=sinx x∈
[0,π
], y=3sinx x∈
[0,π
] (por. Rys. 15.8)
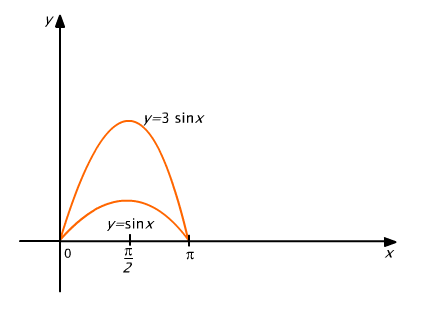
Rys. 15.8
Obszar D nie jest normalny względem osi Oy, ale jest normalny względem osi Ox.
Rzutem zbioru D na oś Ox jest odcinek [0,π ]. Górny brzeg zbioru D ma równanie y=3sinx, a dolny brzeg ma równanie y=sinx.
Zatem D jako obszar normalny względem osi Ox ma opis ![]()
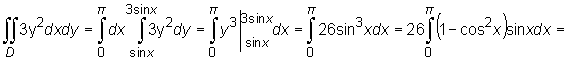
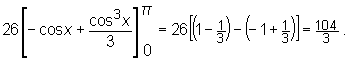
W trakcie obliczeń skorzystaliśmy z tego, że
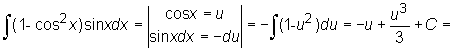
![]()
Przykład
Obliczmy całkę ![]() gdzie D jest obszarem ograniczonym łukami parabol
gdzie D jest obszarem ograniczonym łukami parabol ![]()
Z układu równań 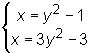 wyznaczamy punkty przecięcia parabol: A=(0,1), B=(0,-1). Szkicujemy obszar D (por. Rys. 15.9) i korzystając z rysunku zauważamy, że nie jest on normalny względem osi Ox, ale jest normalny względem osi Oy.
wyznaczamy punkty przecięcia parabol: A=(0,1), B=(0,-1). Szkicujemy obszar D (por. Rys. 15.9) i korzystając z rysunku zauważamy, że nie jest on normalny względem osi Ox, ale jest normalny względem osi Oy.
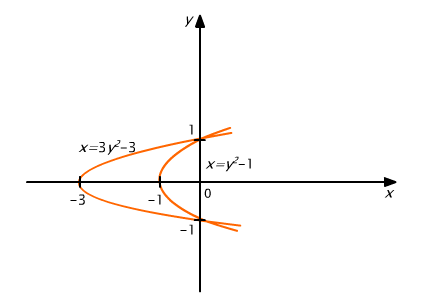
Rys. 15.9
Rzutem zbioru D na oś Oy jest odcinek [-1,1]. Lewy brzeg zbioru D to krzywa o równaniu ![]() , a prawy brzeg krzywa o równaniu
, a prawy brzeg krzywa o równaniu ![]()
Zatem
![]()
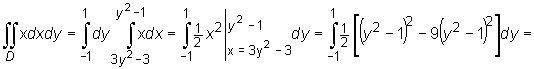
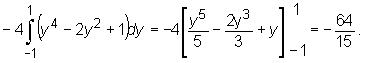
W poniższej definicji i w poniższym twierdzeniu przez obszar normalny rozumiemy zbiór który jest obszarem normalnym względem osi Ox lub względem osi Oy.
Definicja (obszar regularny)
Obszar D⊂ R2 nazywamy obszarem regularnym, jeśli jest on sumą skończonej liczby obszarów normalnych o parami rozłącznych wnętrzach.
Na Rys. 15.10 naszkicowanych jest kilka obszarów regularnych i ich rozbić na obszary normalne.
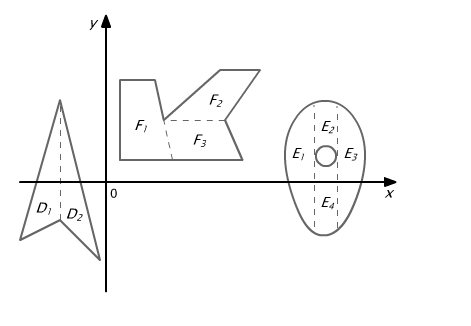
Rys. 15.10
Twierdzenie
Niech ![]() gdzie
gdzie ![]() są obszarami normalnymi o parami rozłącznych wnętrzach, będzie obszarem regularnym oraz niech f będzie funkcją ciągłą na obszarze D. Wtedy f jest całkowalna na D oraz
są obszarami normalnymi o parami rozłącznych wnętrzach, będzie obszarem regularnym oraz niech f będzie funkcją ciągłą na obszarze D. Wtedy f jest całkowalna na D oraz
![]()
Rozbicie obszaru D na sumę obszarów przeprowadzamy również w przypadku, gdy jest on normalny, ale któraś z funkcji których wykresy ograniczają D jest zadana więcej niż jednym wzorem. Mówi o tym poniższa:
Uwaga
Jeśli obszar D jest normalny względem osi Ox, ale jego górny lub dolny brzeg składa się z kilku kawałków będących wykresami różnych funkcji tj. opisanych różnymi równaniami to należy rozbić obszar D prostymi równoległymi do osi Oy na obszary D1,..., Dk w taki sposób, aby każdy z tych podobszarów miał górny brzeg opisany jednym równaniem i dolny brzeg opisany jednym równaniem. Np. dla obszaru D naszkicowanego na Rys. 15.11 wyliczenie po nim całki podwójnej przeprowadzamy w następujący sposób:
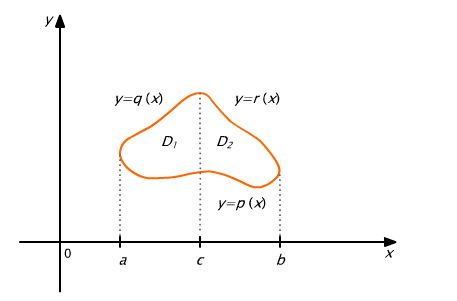
Rys. 15.11
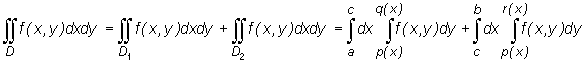
Podobnie, gdy obszar D jest normalny względem osi Oy, ale jego lewy lub prawy brzeg składa się z kilku kawałków będących wykresami różnych funkcji tj. opisanych różnymi równaniami, to należy rozbić obszar D prostymi równoległymi do osi Ox na obszary D1,..., Dk w taki sposób, aby każdy z tych podobszarów miał lewy brzeg opisany jednym równaniem i prawy brzeg opisany jednym równaniem. Np. dla obszaru D naszkicowanego na Rys. 15.12 wyliczenie po nim całki podwójnej przeprowadzamy w następujący sposób:
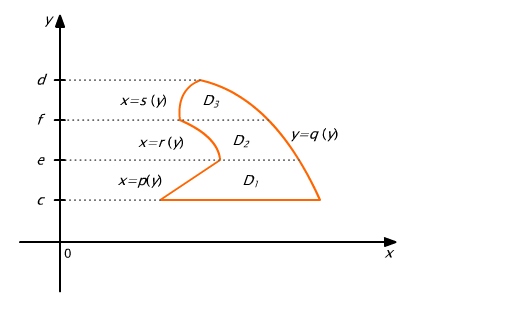
Rys. 15.12
![]()
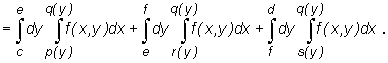
Przykład
Obliczymy ![]() , gdzie D jest obszarem ograniczonym łukami krzywych y=x2,
, gdzie D jest obszarem ograniczonym łukami krzywych y=x2,
y=2+⎟ x⎟.
Z układów równań 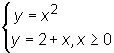 dostajemy x = 2. Z układu równań
dostajemy x = 2. Z układu równań 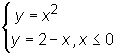 dostajemy x = -2. Szkicujemy rysunek obszaru D (por. Rys. 15.13).
dostajemy x = -2. Szkicujemy rysunek obszaru D (por. Rys. 15.13).
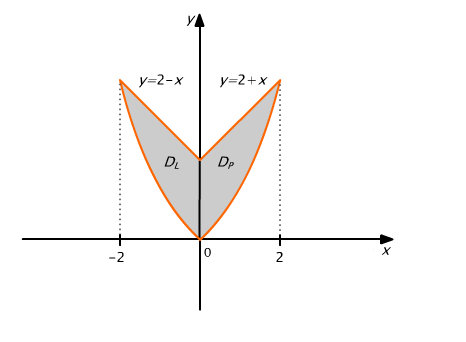
Rys. 15.13
Górny brzeg obszaru D opisany jest równaniem ![]() Dlatego rozbijamy obszar D prostą x=0 na 2 podobszary:
Dlatego rozbijamy obszar D prostą x=0 na 2 podobszary: ![]()
Zatem
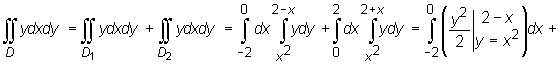
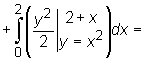
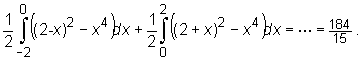
| ↔ poprzedni punkt | następny punkt ≈ |