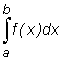 ma naturalną interpretację jako pole obszaru ograniczonego od dołu odcinkiem [a,b] osi Ox , a od góry wykresem funkcji f(x), x∈
[a,b].
ma naturalną interpretację jako pole obszaru ograniczonego od dołu odcinkiem [a,b] osi Ox , a od góry wykresem funkcji f(x), x∈
[a,b]. | ↔ poprzedni punkt | następny punkt ≈ |
Jak już wiemy, w przypadku całki Riemanna funkcji jednej zmiennej można wykazać, że jeżeli f jest funkcją ciągłą na przedziale [a,b] przy czym f(x) ≥
0 dla każdego x∈
[a,b], to 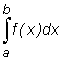 ma naturalną interpretację jako pole obszaru ograniczonego od dołu odcinkiem [a,b] osi Ox , a od góry wykresem funkcji f(x), x∈
[a,b].
ma naturalną interpretację jako pole obszaru ograniczonego od dołu odcinkiem [a,b] osi Ox , a od góry wykresem funkcji f(x), x∈
[a,b].
Podobnie jeżeli f oraz g są funkcjami ciągłymi na przedziale [a,b] przy czym f(x)≤
g(x) dla x∈
[a,b], to całka 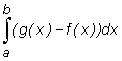 ma naturalną interpretację jako pole obszaru ograniczonego od dołu wykresem funkcji f(x), x∈
[a,b], a od góry wykresem funkcji g(x), x∈
[a,b].
ma naturalną interpretację jako pole obszaru ograniczonego od dołu wykresem funkcji f(x), x∈
[a,b], a od góry wykresem funkcji g(x), x∈
[a,b].
Podobnie w przypadku dwuwymiarowym można wykazać, że jeżeli f jest funkcją ciągłą na obszarze regularnym D⊂ R2 przy czym f(x,y)≥ 0 dla (x,y)∈ D oraz V jest bryłą o kształcie słupa ograniczonego od dołu powierzchnią D zawartą w płaszczyźnie Oxy,
a od góry powierzchnią o równaniu z=f(x,y), (x,y)∈
D (por. Rys. 15.14), to znaczy ![]() , to objętość ⏐
V⏐
tej bryły wyraża się wzorem:
, to objętość ⏐
V⏐
tej bryły wyraża się wzorem:
![]()
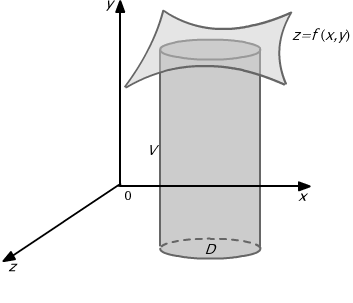
Rys. 15.14
Przyjmując f(x,y)=1, ∀ (x,y)∈ D otrzymujemy stąd następujący wzór na pole | D| obszaru D :
![]()
(bo objętość takiego słupa o stałej wysokości 1 jest równa polu jego podstawy).
Podobnie jeżeli f oraz g są funkcjami ciągłymi na obszarze D przy czym f(x)≤
g(x) dla każdego (x,y)∈
D, zaś V jest bryłą o kształcie słupa ograniczonego od dołu powierzchnią o równaniu z=f(x,y), (x,y)∈
D, a od góry powierzchnią o równaniu z=g(x,y), (x,y)∈
D (por. Rys.15.15), czyli ![]() , to objętość bryły V wyraża się wzorem:
, to objętość bryły V wyraża się wzorem:
![]()
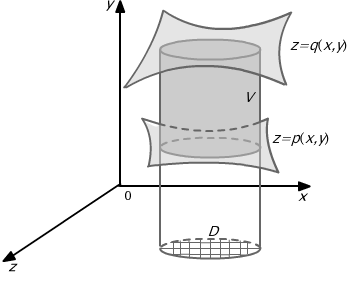
Rys. 15.15
Przykład
Obliczmy za pomocą całki podwójnej pole obszaru D ograniczonego łukami krzywych y=2x, xy=2, y=6 (por. Rys. 15.16)
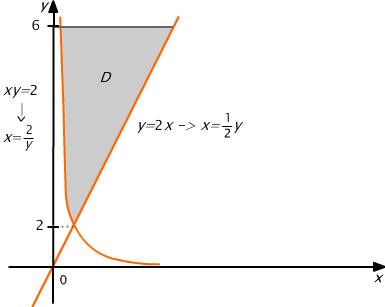
Rys. 15.16
Mamy:
![]()
Obszar D jest normalny względem osi Oy i jako obszar normalny względem tej osi ma następujący opis: ![]() Zatem :
Zatem :
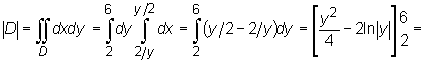
![]()
Przykład
Obliczmy za pomocą całki podwójnej pole obszaru D ograniczonego łukami krzywych
y
=x2-2x, y− x=0.Mamy:
![]()
Wyznaczamy punkty wspólne obu krzywych ograniczających obszar D:
x= x2-2x ⇔ x2-3x=0 ⇔ x(x-3)=0 ⇔ x=0∨ x=3.
Szkicujemy obszar D (rys. 15.17).
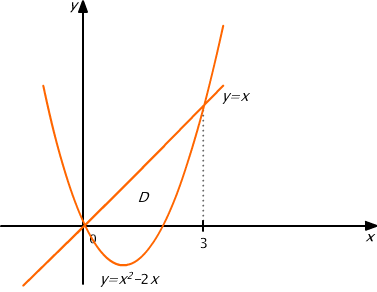
Rys. 15.17
Obszar ten jest normalny względem osi Oy , lecz wygodniej jest traktować go jako obszar normalny względem osi Ox gdyż jego lewy brzeg jest sumą dwóch krzywych opisanych różnymi równaniami. A zatem : D: 0≤
x≤
3, x2-2x ≤
y ≤
x, skąd 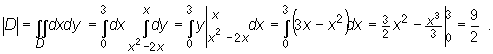
Przykład
Obliczmy za pomocą całki podwójnej objętość bryły ![]() , gdzie D jest podzbiorem płaszczyzny Oxy ograniczonym odcinkami prostych y=2x, y=x, x=2.
, gdzie D jest podzbiorem płaszczyzny Oxy ograniczonym odcinkami prostych y=2x, y=x, x=2.
Mamy ![]() (por. Rys. 15.18).
(por. Rys. 15.18).
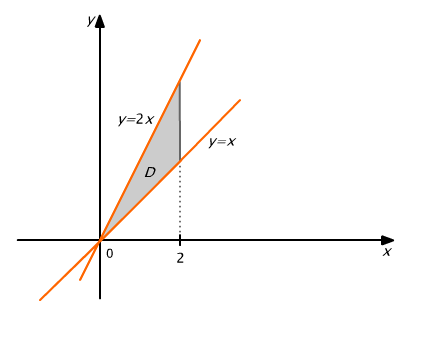
Rys. 15.18
Zatem
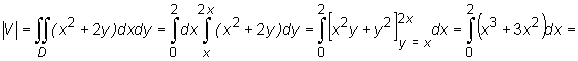
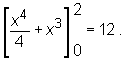
Przykład
Obliczmy za pomocą całki podwójnej objętość bryły ![]() , gdzie D jest podzbiorem pierwszej ćwiartki płaszczyzny Oxy ograniczonym łukami krzywych
, gdzie D jest podzbiorem pierwszej ćwiartki płaszczyzny Oxy ograniczonym łukami krzywych ![]() (por.Rys.15.19).
(por.Rys.15.19).
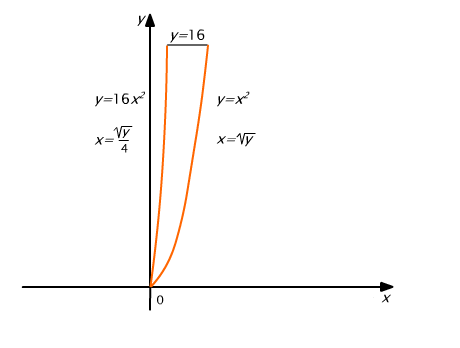
Rys. 15.19
Mamy ![]() . Zatem
. Zatem
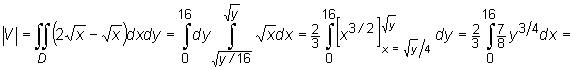
![]()
| ↔ poprzedni punkt | następny punkt ≈ |