| następny punkt ≈ |
Niech an, n = 1, 2,..., będzie ciągiem liczbowym. Dla ustalonego n, niech Sn oznacza sumę n początkowych wyrazów ciągu (an). Stąd
S1 = a1, S2 = a1 + a2, S3 = a1 + a2 + a3, i ogólnie
![]()
Definicja
Szereg ![]() jest ciągiem (Sn) swoich sum częściowych.
jest ciągiem (Sn) swoich sum częściowych.
Definicja
Fakt, że ![]() zapisujemy często symbolicznie
zapisujemy często symbolicznie
![]()
Ostatnia równość ma charakter umowny, bo szereg i suma szeregu to pojęcia różne oznaczane tym samym symbolem ![]()
Przykład
Rozważmy szereg, którego n-ty wyraz an = 1/2n. Zatem jest to szereg
![]()
Ciąg sum częściowych (Sn) ma wyraz ogólny
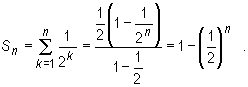
Zatem

czyli S = 1, co zapisujemy symbolicznie
![]()
Pytanie kontrolne 2.1
Oblicz sumę szeregu 
Przykład
Pokażemy, że rozbieżny jest szereg − 1 + 1 − 1 + ... + (− 1)n + ..., czyli szereg
![]()
Ciąg (Sn) sum częściowych tego szeregu ma dwa podciągi zbieżne do dwóch różnych granic. Podciąg złożony z wyrazów o indeksach parzystych ma wszystkie wyrazy równe 0, bo dla n = 2k mamy
![]()
Podciąg zawierający wyrazy ciągu (Sn) o indeksach nieparzystych ma wyrazy równe − 1, gdyż dla n = 2k − 1 mamy
![]()
Zatem ciąg (Sn) jest rozbieżny. Nie może on być zbieżnym, gdyż podciągi każdego ciągu zbieżnego mają jednakowe granice równe granicy tego ciągu.
Przykład
Zbadajmy zbieżność szeregu
![]()
![]()
![]()
Stąd
![]()
Pokazaliśmy, że badany szereg jest zbieżny i jego suma wynosi 1, co w skrócie zapisujemy:
![]()
Jeżeli w szeregu ![]() pominiemy n początkowych wyrazów, to otrzymamy szereg
pominiemy n początkowych wyrazów, to otrzymamy szereg
![]()
który nazywamy n-tą resztą szeregu ![]() .
.
Twierdzenie (o zbieżności reszty szeregu zbieżnego)
Szereg ![]() i szereg
i szereg ![]() mają tę własność, że dla każdego n są obydwa zbieżne albo obydwa rozbieżne, tzn. dla dowolnego n
mają tę własność, że dla każdego n są obydwa zbieżne albo obydwa rozbieżne, tzn. dla dowolnego n
![]() zbieżny ⇔
zbieżny ⇔
![]() zbieżny.
zbieżny.
Uwaga
Jeśli w szeregu zbieżnym pominiemy skończoną liczbę początkowych wyrazów, to sumy obu szeregów na ogół będą różne, na przykład
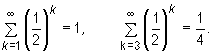
Definicja
Uwaga
Zbieżność szeregów zapewnia zbieżność ich sumy, ale twierdzenie odwrotne nie zachodzi - suma szeregów rozbieżnych może być szeregiem zbieżnym.
Przykład
Niech an = n, bn = − n, n = 1, 2,...
Szeregi
![]()
są rozbieżne, ale suma tych szeregów ma n-ty wyraz an + bn = 0, czyli jest szeregiem 0 + 0 + 0 + 0 + ... mającym sumę 0.
Twierdzenie (o sumie szeregów zbieżnych oraz o sumie iloczynu liczby i szeregu zbieżnego)
Jeżeli szeregi ![]() są zbieżne oraz ich sumy wynoszą odpowiednio A i B,
są zbieżne oraz ich sumy wynoszą odpowiednio A i B,
to szeregi ![]()
![]() są zbieżne, a ich sumy wynoszą
są zbieżne, a ich sumy wynoszą
![]()
gdzie a jest dowolną liczbą.
Przykład
Obliczymy sumę szeregu:



Pytanie kontrolne 2.2
Oblicz sumę szeregu

Pytanie kontrolne 2.3
Czy zbieżny jest szereg
![]()
Uwaga
Warunek ![]() nie jest warunkiem wystarczającym zbieżności szeregu
nie jest warunkiem wystarczającym zbieżności szeregu ![]() . Może on zachodzić dla szeregu rozbieżnego.
. Może on zachodzić dla szeregu rozbieżnego.
Dowód
Wykażemy rozbieżność szeregu harmonicznego stosując metodę dowodu nie wprost. Załóżmy przeto, że szereg harmoniczny ![]() jest zbieżny.
jest zbieżny.
Wówczas dla każdego k zbieżna jest także k-ta reszta, czyli szereg![]()
Jeżeli oznaczymy ![]() (1)
(1)
co pokazaliśmy w dowodzie warunku koniecznego zbieżności szeregu.
Jeśli n spełnia nierówności k + 1 ≤ n ≤ 2k, to 1/n ≥ (1/2)k, skąd sumując obie strony ostatniej nierówności po n od k + 1 do 2k otrzymamy
![]()
Stąd dla N > 2k mamy
![]()
skąd
![]()
Zatem ![]() co sprzeczne jest z równością (1) wynikającą z założenia o zbieżności szeregu. Szereg harmoniczny jest więc rozbieżny.
co sprzeczne jest z równością (1) wynikającą z założenia o zbieżności szeregu. Szereg harmoniczny jest więc rozbieżny.
Pytanie kontrolne 2.4
Niech c będzie dowolną stałą różną od zera. Czy zbieżny jest szereg
![]()
Przykład
Zbadamy warunki zbieżności szeregu geometrycznego
![]()
Ponieważ

Szereg geometryczny jest w tym przypadku zbieżny i jego sumą jest liczba a / (1− q), czyli
![]()
Ponieważ dla każdego naturalnego n mamy
![]()
więc nie jest spełniony warunek konieczny zbieżności szeregu. Szereg ![]() jest rozbieżny.
jest rozbieżny.
Z rozumowania w powyższym przykładzie otrzymujemy
| następny punkt ≈ |