Przykład

Pokażemy, że szereg jest zbieżny. Jest to szereg naprzemienny, gdzie

Zatem ciąg (a_n) jest nierosnący. Spełnione są założenia kryterium Leibniza, więc szereg jest zbieżny.

Pytanie kontrolne 2.9

Wykaż, że szereg jest zbieżny.

Przykład

Szereg jest zbieżny na mocy kryterium Leibniza. Ponadto, ponieważ szereg

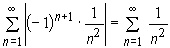
także jest zbieżny, więc szereg

jest zbieżny bezwzględnie.

Uwaga

Twierdzenie odwrotne nie jest prawdziwe.

Przykład

Szereg jest zbieżny na mocy kryterium Leibniza, natomiast nie jest zbieżny bezwzględnie, gdyż szereg modułów jego wyrazów, równych ⎮ (− 1)ⁿ+1/n ⎮ = 1/n, jest szeregiem harmonicznym, więc rozbieżnym.

Przykład

Zbadamy zbieżność szeregu .

Rozważmy szereg utworzony z bezwzględnych wartości wyrazów badanego szeregu, czyli szereg

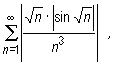
dla którego zastosujemy kryterium porównawcze. Dla każdego naturalnego n

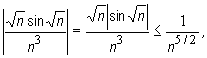
więc szereg 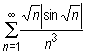jest zbieżny, gdyż zbieżny jest szereg Dirichleta

czyli szereg jest zbieżny bezwzględnie, zatem jest też zbieżny na podstawie ostatniego twierdzenia.

Pytanie kontrolne 2.10

Wykaż, że szereg 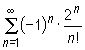jest zbieżny.

Przykład

Wykażemy, że szereg jest zbieżny dla każdej liczby x.

Na mocy twierdzenia o zbieżności szeregu bezwzględnie zbieżnego wystarczy wykazać zbieżność bezwzględną badanego szeregu dla dowolnego x, to znaczy zbieżność szeregu

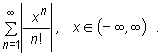
Rozważmy dwa przypadki:

• x = 0 ⇒ szereg jest zbieżny i ma sumę równą 0.
• Niech x ≠ 0. Wówczas

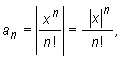
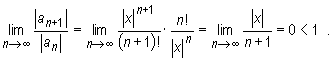
Stąd na podstawie kryterium d'Alemberta szereg jest zbieżny.

Zatem szereg jest zbieżny bezwzględnie dla

Jest więc zbieżny dla wszystkich liczb rzeczywistych x.

Poniższe twierdzenie ilustruje zastosowanie szeregów liczbowych.

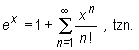
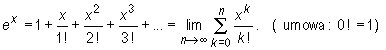
Przykład

Niech x > 0. Wykorzystując twierdzenie pokażemy, że

Liczba e^x jest sumą szeregu :

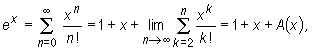
gdzie A(x) > 0, ponieważ wszystkie wyrazy 2-ej reszty szeregu o wyrazach xⁿ / n! są dodatnie przy x > 0.

Z powyższych równości otrzymujemy

Pytanie kontrolne 2.11

Czy jest zbieżny szereg

↔ poprzedni punkt