| następny punkt ≈ |
Napis f : A → B oznacza, że f jest funkcją określoną na zbiorze A o wartościach w zbiorze B. Przez funkcję, o ile nie jest powiedziane inaczej, rozumiemy funkcję o wartościach rzeczywistych. Często dziedzinę funkcji oznaczamy Df. Jeśli funkcja jest zadana wzorem to (o ile nie jest powiedziane inaczej) przez jej dziedzinę rozumiemy dziedzinę naturalną, to jest największy zbiór na którym ten wzór określa funkcję. Złożenie funkcji f : A → B oraz g : C → D oznaczamy
Funkcję odwrotną do funkcji f oznaczamy symbolem f− 1. Zakładamy, że Czytelnik zna ze szkoły podstawowe własności funkcji, a zwłaszcza funkcji potęgowych, wykładniczych, logarytmicznych i trygonometrycznych. Symbolem ln oznaczamy logarytm naturalny tj. funkcję logarytmiczną przy podstawie e ≈ 2,718.
Jeśli f : A→ B oraz C ⊂ A to zawężając dziedzinę funkcji f do zbioru C otrzymujemy nową funkcję oznaczaną f⎮C nazywaną obcięciem f do zbioru C. Jeśli to obcięcie jest funkcją różnowartościową, to istnieje funkcja odwrotna do f⎮C. Na przykład funkcja f(x) = x2, f : R → R nie ma funkcji odwrotnej, a jej obcięcia f1 = f⎮[0, ∞ ) oraz f2 = f⎮[− ∞, 0 ) są różnowartościowe i mają funkcje odwrotne
W podobny sposób definiujemy tak zwane funkcje cyklometryczne, które krótko omówimy poniżej.
Funkcje trygonometryczne sinus, kosinus, tangens i kotangens nie są różnowartościowe, a zatem nie mają funkcji odwrotnych. Jednak obcinając je do przedziałów [-π ⁄ 2, π ⁄ 2] dla sinusa, [0, π ] dla cosinusa oraz (-π ⁄ 2, π ⁄ 2) i (0, π ) dla tangensa i kotangensa odpowiednio, otrzymujemy funkcje różnowartościowe które mają funkcje odwrotne.
Definicja
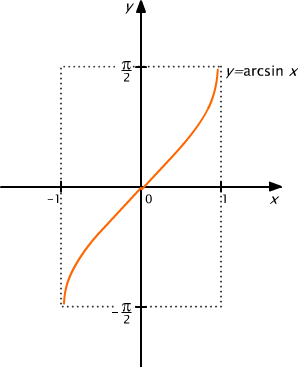
Funkcję odwrotną do funkcji sin⏐[− π / 2, π / 2] nazywamy arkusem sinusem i oznaczamy symbolem arcsin.
Rys. 3.1
Z definicji wynika, że Darcsin = [-1,1] oraz, że dla x ∈ [-1,1]
arcsin(x) = y ⇔ (sin(y) = x ∧ y ∈ [-π ⁄ 2, π ⁄ 2] ).
Definicja
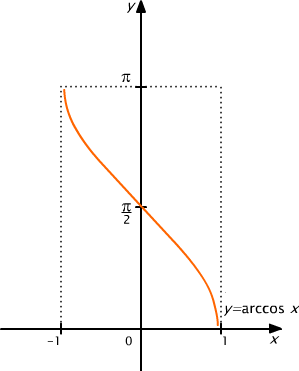
Funkcję odwrotną do funkcji cos⏐[0, π ] nazywamy arkusem kosinusem i oznaczamy symbolem arccos.
Rys. 3.2
Z definicji wynika, że Darccos = [-1,1] oraz, że dla x ∈ [-1,1]
arccos(x) = y ⇔ (sin(y) = x ∧ y ∈ [0, π ] ).
Definicja
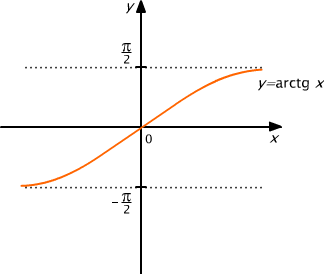
Funkcję odwrotną do funkcji tg⏐(− π / 2, π / 2) nazywamy arkusem tangensem i oznaczamy symbolem arctg.
Rys. 3.3
Z definicji wynika, że Darctg = (-∞, ∞ ) oraz, że dla x ∈ (-∞, ∞ )
arctg(x) = y ⇔ (tg(y) = x ∧ y ∈ (-π ⁄ 2, π ⁄ 2)).
Definicja
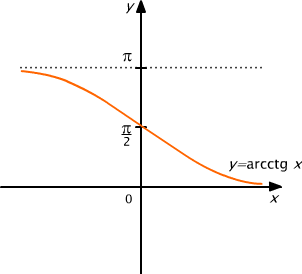
Funkcję odwrotną do funkcji ctg⏐(0, π ) nazywamy arkusem kotangensem i oznaczamy symbolem arcctg.
Rys. 3.4
Z definicji wynika, że Darcctg = (-∞, ∞ ) oraz, że dla x ∈ (-∞, ∞ )
arctg(x) = y ⇔ (ctg(y) = x ∧ y ∈ (0, π )).
Definicja
Podstawowymi funkcjami elementarnymi nazywamy funkcje : stałe, potęgowe, wykładnicze, logarytmiczne, trygonometryczne oraz cyklometryczne. (Pierwiastki też są podstawowymi funkcjami elementarnymi, bo są funkcjami potęgowymi)
Funkcjami elementarnymi
nazywamy podstawowe funkcje elementarne i wszystkie funkcje, które można otrzymać z podstawowych funkcji elementarnych za pomocą skończonej liczby działań arytmetycznych i operacji składania funkcji.Przykłady
wynika, że funkcja g(x) = xtgx jest elementarna.
wynika, że funkcja h(x) =⎮ x⎮ jest elementarna.
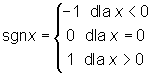
nie jest elementarna.
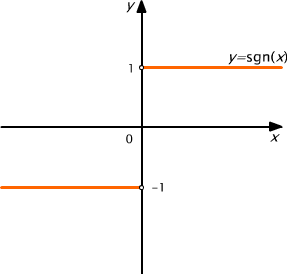
Rys. 3.5
Definicja
Niech x0 ∈ R, ε >0. Otoczeniem x0 o promieniu ε nazywamy odcinek
Prawostronnym otoczeniem x0 o promieniu ε
nazywamy zbiór
zaś lewostronnym otoczeniem zbiór 
Zbiór S(x0, ε ) = ( x0-ε, x0)∪ ( x0, x0+ε ) nazywamy sąsiedztwem punktu x0 o promieniu ε. Ponadto przyjmijmy jeszcze następujące oznaczenia:
- sąsiedztwo lewostronne x0 o promieniu ε,
- sąsiedztwo prawostronne x0 o promieniu ε.
Jeśli promień otoczenia lub sąsiedztwa nie jest istotny, to zamiast pisać
piszemy odpowiednio
Sąsiedztwem -∞ nazywać będziemy półprostą S(-∞ ) = (-∞, b) gdzie b∈ R.
Sąsiedztwem ∞ nazywać będziemy półprostą S(∞) = (a, ∞ ) gdzie a∈ R.
| następny punkt ≈ |