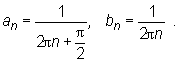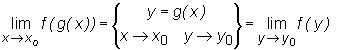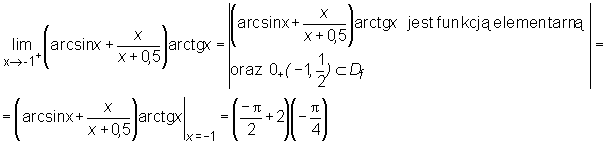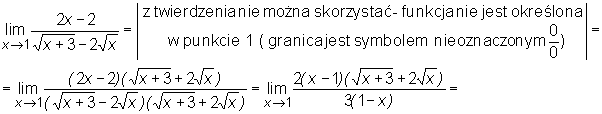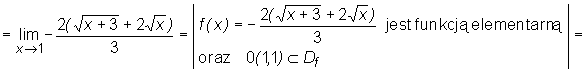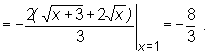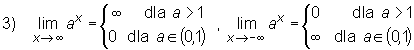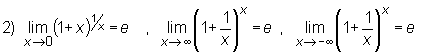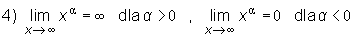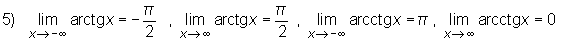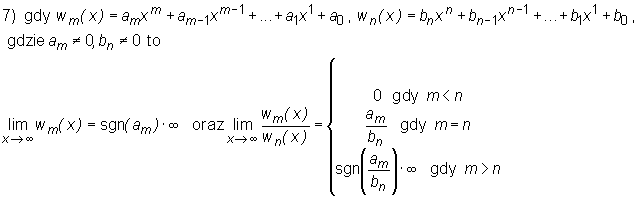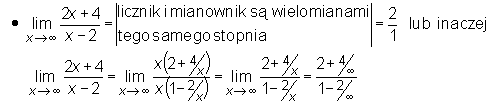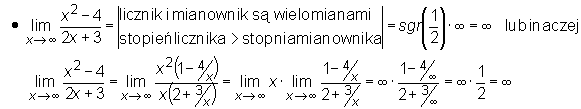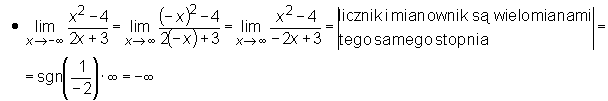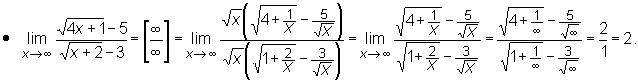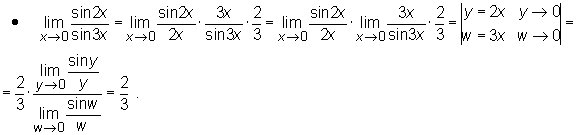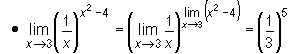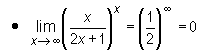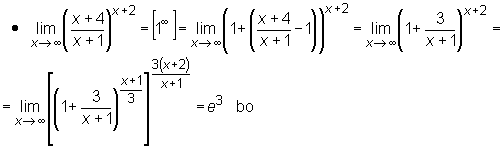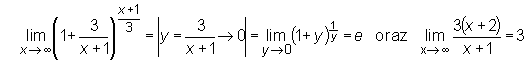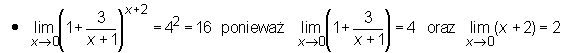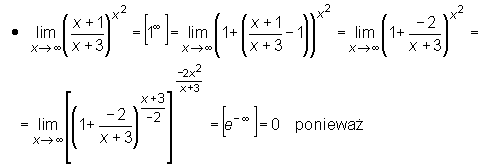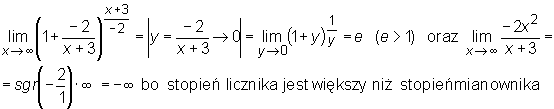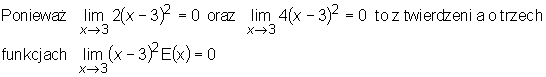2. GRANICA FUNKCJI
Definicja (Heine)
Niech x0 ∈
R∪
{-∞, ∞
}. Niech f będzie funkcją określoną na pewnym sąsiedztwie S(x0) punktu x0. Powiemy, że g ∈
R∪
{-∞, +∞
} jest granicą funkcji f w punkcie x0 jeśli spełniony jest warunek:
dla każdego ciągu (xn), elementów sąsiedztwa S(x0), o granicy x0
ciąg (f(xn)) ma granicę g.
Fakt, że g jest granicą funkcji f w punkcie x0 oznaczamy symbolem
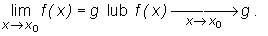
Jeśli g ∈
R, to mówimy, że granica jest właściwa. Jeśli g ∈
{-∞, +∞
}, to mówimy, że granica jest niewłaściwa.
Można pokazać, że jeśli istnieje granica (bądź granica jednostronna) funkcji w punkcie to jest ona wyznaczona jednoznacznie tj. funkcja nie może mieć dwóch różnych granic w punkcie.
Zauważmy, że z ostatniej definicji wypływa prosty, jednak bardzo przydatny
Wniosek
Jeżeli w S(x0) istnieją dwa ciągi (an) , (bn) , oba o granicy x0 oraz granice ciągów (f(an)), (f(bn)) są różne, to granica funkcji f w punkcie x0 nie istnieje.
Przykład
Korzystając z ostatniego wniosku wykażemy, że granica funkcji y = sin(1/x) w punkcie x0 = 0 nie istnieje. Rozpatrzmy ciągi o wyrazach ogólnych
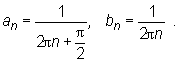
Oczywiście oba te ciągi są zbieżne do 0. Jednak granicą ciągu (
sin(1/an))
jest 1, zaś granicą ciągu (
sin(1/bn))
jest 0.
Definicja
Niech x0 ∈
R i niech f będzie funkcją określoną (przynajmniej) na pewnym lewostronnym sąsiedztwie  punktu x0.
punktu x0.
Powiemy, że g ∈
R∪
{−
∞,∞
} jest granicą lewostronną funkcji f w punkcie x0 jeśli spełniony jest warunek :
dla każdego ciągu (xn), elementów lewostronnego sąsiedztwa S−
(x0), zbieżnego do x0 ciąg (f(xn)) jest zbieżny do g.
Fakt, że g jest granicą lewostronną funkcji f w punkcie x0 zapisujemy jednym z symboli:
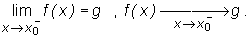
Analogicznie definiuje się granicę prawostronną funkcji w punkcie ( stosujemy oznaczenie:
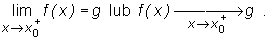
Granice lewostronną oraz prawostronną nazywamy granicami jednostronnymi.
Związek między granicą funkcji w punkcie a granicami jednostronnymi podaje następujące
Twierdzenie
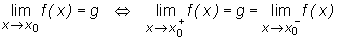 .
.
Poniższe twierdzenie podaje warunek równoważny definicji Heinego granicy właściwej funkcji w punkcie x0 ∈
R, nazywany definicją Cauchy'ego.
Twierdzenie
Niech x0, g ∈
R. Niech f będzie funkcją określoną na pewnym sąsiedztwie S(x0) punktu x0. Wówczas
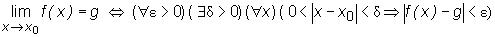
W podobny sposób można sformułować, przy użyciu symboli nierówności i ewentualnie wartości bezwzględnej, około 11 warunków nazywanych definicjami Cauchy'ego równoważnych definicji Heinego (granica -∞
w punkcie x0 ∈
R, granica lewostronna -∞
w punkcie x0 ∈
R, ...., granica właściwa w ∞
,...). Na szczęście dla Czytelnika na tym wykładzie nikt nie będzie wymagać ich znajomości.
Często jest używane, prawie zawsze bez powołania się na nie, następujące
Twierdzenie
Jeśli funkcje f, g są takie, że
(1)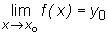
(2) (∃
δ
>
0) (∀
x) 0<
⎥
x−
x0⏐
<
δ
⇒
f(x)≠
y0
(3)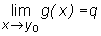
to 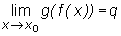 .
.
Gdy licząc granicę mówimy, że stosujemy zamianę zmiennych lub piszemy
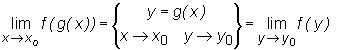
bądź podobne wyrażenie to stosujemy właśnie to twierdzenie.
Poniższe twierdzenie ułatwia liczenie granic. Pułapki spotykamy, gdy nie są spełnione jego założenia: gdy funkcja nie jest elementarna (np. czasem gdy jest określona kilkoma różnymi wzorami) bądź gdy funkcja nie jest określona w punkcie x0 (najczęściej w przypadku gdy granica jest symbolem nieoznaczonym).
Twierdzenie
Niech f będzie funkcją elementarną. Wówczas
1) 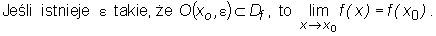
2) 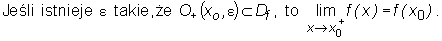
3) 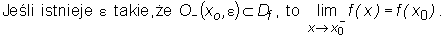
Przykład
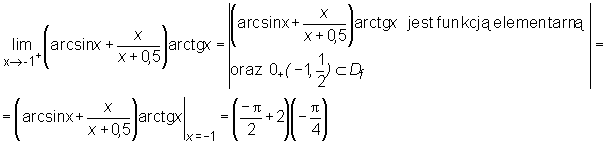
Przykład
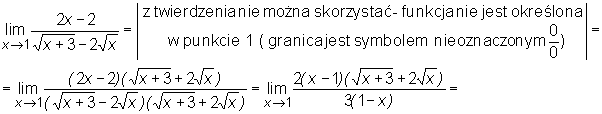
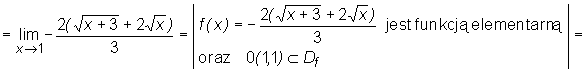
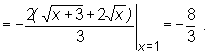
Uwaga
W rozwiązaniach zadań komentarze takie jak w obu poprzednich przykładach są domyślne i na ogół nie są wypisywane.
Związek między działaniami arytmetycznymi a granicami funkcji podaje następujące:
Uwaga
Twierdzenie powyższe pozostaje prawdziwe dla granic jednostronnych . Ponadto w przypadku gdy co najmniej jedna z granic jest niewłaściwa to prawdziwe pozostają odpowiedniki odpowiednich reguł dla granic ciągów.
Następne twierdzenie podaje kilka ważnych granic które należy zapamiętać:
Twierdzenie
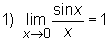
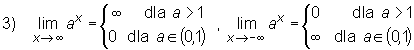
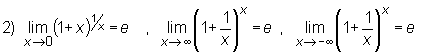
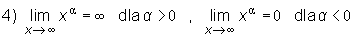
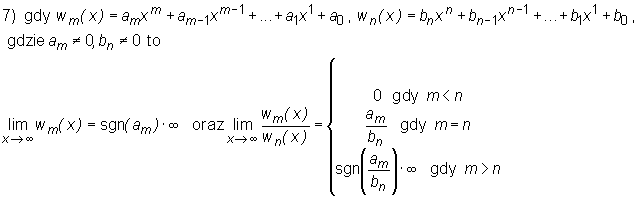
granice 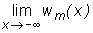 oraz
oraz 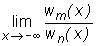 możemy wyznaczyć korzystając z wzoru
możemy wyznaczyć korzystając z wzoru
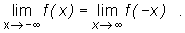
Przykład
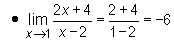
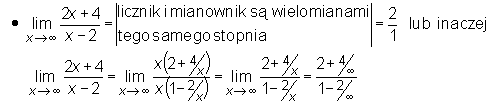
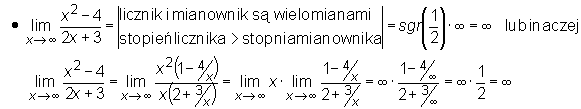
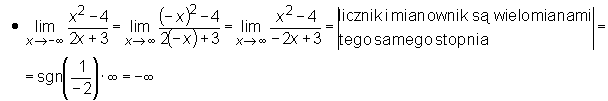
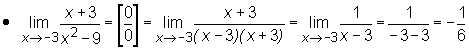

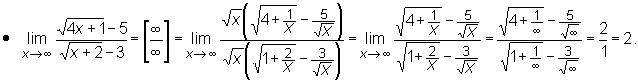
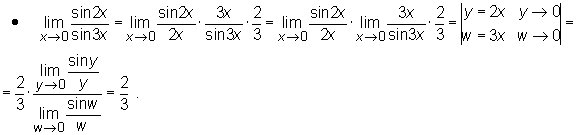
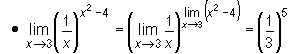
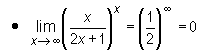
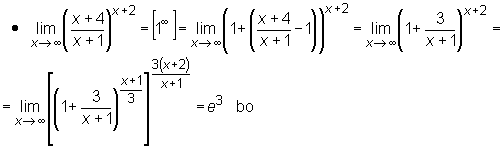
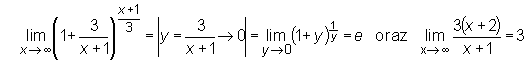
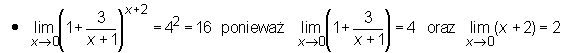
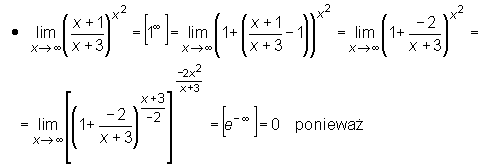
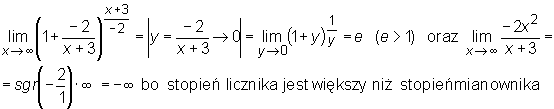
Przy wyznaczaniu granic użyteczne są następujące dwa twierdzenia
Twierdzenie (o dwóch funkcjach)
Jeśli funkcje f, g są takie, że
(1) f(x) ≤
g(x) w pewnym sąsiedztwie S(x0) punktu x0 ∈
R∪
{−
∞, ∞
}
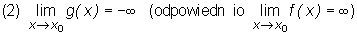
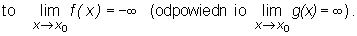
Analogiczne twierdzenie jest prawdziwe dla granic jednostronnych.
Przykład
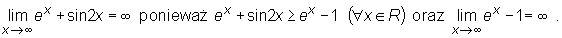
Twierdzenie (o trzech funkcjach)
Jeśli funkcje f1, f2, f3 spełniają warunki:
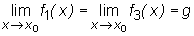
- istnieje sąsiedztwo S(x0) punktu x0 takie, że f1(x)≤
f2(x)≤
f3(x) ∀
x∈
S(x0),
to 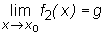 .
.
Twierdzenie to pozostaje prawdziwe również dla granic jednostronnych.
Przykład
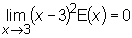
Rzeczywiście 2 ≤
E(x) ≤
4 (∀
x ∈
S(3, 1)=(2, 4) )
Zatem
2(x−
3)2 ≤
(x−
3)2 ≤
4(x−
3)2 (∀
x ∈
S(3, 1)=(2, 4) )
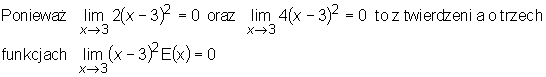
Bezpośrednim wnioskiem z twierdzenia o trzech funkcjach jest następujące o iloczynie funkcji zbieżnej do zera przez funkcję ograniczoną:
Twierdzenie
Jeżeli funkcja g(x) jest ograniczona w pewnym otoczeniu S(x0) punktu x0 oraz
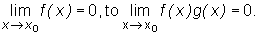
Przykład

Czasem przydatne bywa twierdzenie o zachowywaniu znaku przy przejściu do granicy:
Twierdzenie
Jeżeli istnieje takie otoczenie S(x0) punktu x0, że f(x) ≤
g(x) dla dowolnego x0 ∈
S(x0), to
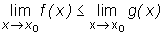 .
.
![]()