Definicja
Powiemy, że funkcja f ma w punkcie x0 ∈ R pochodną (właściwą), jeśli
a) istnieje ε > 0 takie, że O(x0, ε )⊂ Df ,
b) istnieje właściwa granica
| ↔ poprzedni punkt | następny punkt ≈ |
Definicja
Powiemy, że funkcja f ma w punkcie x0 ∈ R pochodną (właściwą), jeśli
a) istnieje ε > 0 takie, że O(x0, ε )⊂ Df ,
b) istnieje właściwa granica
Granicę tę nazywamy pochodną funkcji f w punkcie x0 i oznaczamy jednym z symboli:
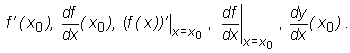
Definicja
Jeśli funkcja f ma pochodną w punkcie x0, to mówimy, że f jest różniczkowalna w punkcie x0. Jeśli f nie ma pochodnej w punkcie x0 lub ma w tym punkcie pochodną niewłaściwą, to mówimy, że f nie jest różniczkowalna w punkcie x0.
Przykłady
![]()
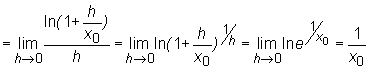
przy czym wykorzystana została równość
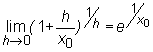

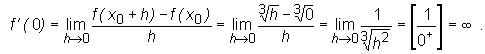
Zatem funkcja ta nie jest różniczkowalna w punkcie x0 = 0, chociaż ma w tym punkcie pochodną niewłaściwą.
Definicja
Niech x0 będzie takim punktem z dziedziny funkcji f, że dla pewnej liczby ε >0 mamy O+ (x0, ε) ⊂ Df . Pochodną prawostronną (właściwą) f '+(x0) funkcji f w punkcie x0 nazywamy granicę prawostronną właściwą
![]() .
.
Analogicznie definiuje się pochodną lewostronną (właściwą) f '- (x0) funkcji f w punkcie x0 :
![]() .
.
Jeśli któraś z powyższych granic istnieje lecz jest niewłaściwa to mówimy o niewłaściwej pochodnej jednostronnej.
Uwaga
Z twierdzeń o granicach wynika, że jeśli funkcja f ma w pewnym punkcie x0 pochodną prawostronną i pochodną lewostronną oraz pochodne te są równe a, to f ma w punkcie x0 pochodną równą a. Jeśli funkcja f ma w pewnym punkcie x0 pochodną równą a, to ma też prawostronną i lewostronną pochodną w punkcie x0 i obie te pochodne są równe a.
| ↔ poprzedni punkt | następny punkt ≈ |