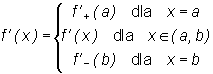↔ poprzedni punkt  następny punkt ≈


5. POCHODNA FUNKCJI I JEJ WŁASNOŚCI

Definicja

Powiemy, że funkcja f jest różniczkowalna w przedziale (a,b), jeśli f jest różniczkowalna w każdym punkcie tego przedziału.

Podobnie mówimy, że funkcja f jest różniczkowalna w przedziale [a,b] , jeśli f jest różniczkowalna w przedziale (a, b) i istnieją właściwe pochodne jednostronne f'+ (a) oraz f'- (b).

Analogicznie można zdefiniować funkcję różniczkowalną w przedziale jednostronnie domkniętym i sformułowanie tej definicji zostawiamy czytelnikowi.

Definicja

Pochodną funkcji f w przedziale (a , b) nazywamy funkcję f' przyjmującą w każdym punkcie x ∈ (a , b) wartość f'(x) .

Pochodną funkcji f w przedziale [a , b] nazywamy funkcję określoną wzorem

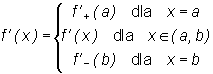Podobnie definiujemy pochodną funkcji w przedziale jednostronnie domkniętym.

Następne twierdzenie podaje podstawowe własności pochodnej funkcji.

Twierdzenie

Jeśli funkcje f, g są różniczkowalne w punkcie x, to

  1. (f + g )' (x) = f' (x) + g' (x),
  2. (f − g )' (x) = f' (x) − g' (x),
  3. (af )' (x) = af' (x) dla każdej liczby a∈ R,
  4. (f⋅ g )' (x) = f' (x)⋅ g(x) + f(x)⋅ g' (x),
  5. jeśli g(x) ≠ 0 i g' (x) ≠ 0, to

    .

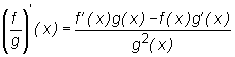Dowód

W dowodzie wykorzystuje się definicję pochodnej funkcji w punkcie. Przykładowo zostanie przeprowadzony dowód punktu 4. Do przeprowadzenia dowodu pozostałych punktów zachęcamy Czytelnika.

Mamy: (f⋅ g )' (x) =


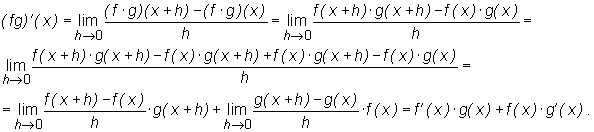
↔ poprzedni punkt  następny punkt ≈