Poniżej podane zostaną wzory na pochodne funkcji elementarnych. Są one prawdziwe wszędzie tam, gdzie obie strony wzoru mają sens. Każdy Student powinien je zapamiętać.

1. c' = 0 dla każdej liczby c∈ R,
2. (xa )' = a ⋅ x^{a -1}, dla każdej niezerowej liczby a,
3. (e^x)' = e^x,
4. (a^x)' = a^x lna , dla każdej liczby a > 0
5. (sin x)' = cos x,
6. (cos x)' = -sin x,
7. (tg x)' = 1/cos² x,
8. (ctg x )' = -1/sin² x.

To, że wzory te są prawdziwe tam gdzie obie stronny wzoru mają sens oznacza, że na przykład:

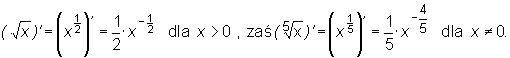
Następne twierdzenie podaje sposób liczenia pochodnej funkcji złożonej.

Przykład

Korzystając z poznanych wzorów na pochodne funkcji elementarnych i ostatniego twierdzenia obliczmy pochodną funkcji

• h(x) = e^tgx

  W oznaczeniach ostatniego twierdzenia f(x) = tg x oraz g(x) = e^x. Stąd

  (g° f) '(x) = [g(f(x))] ' = (e^{tg x})' = e^{tg x} ⋅ (1/ cos² x )

• y = sin (cos x ^1/3)

  Ta funkcja jest złożeniem trzech funkcji : f(x) = x^1/3 , g(x) = cos x , h(x) =sinx. Jak poprzednio mamy:

  y'(x) = (h° g°f)'= h' ((g° f)(x) )⋅(g°f)' (x) = h' ((g° f)(x) )⋅ g' (f(x))⋅ f' (x) =

  = cos (cos x ^1/3) ⋅ (-sin x^1/3) ⋅ (1/3) x ^-2/3.

  

  Ta funkcja jest złożeniem trzech funkcji:

  

  Zatem otrzymujemy

  y' (x) = (h° g° f)' = h' ((g° f)(x) )⋅ (g° f)' (x) = h' ((g° f)(x) )⋅ g' (f(x))⋅ f' (x) =

  

  Z twierdzenia o pochodnej funkcji złożonej otrzymujemy również wzory na pochodne funkcji postaci f(ax) oraz f(ax+b) gdzie a,b ∈ R :

  [(f(ax))]' = af' (ax)

  [(f(ax+b))]' = af' (ax+b)

  Przykład

  

  

  Kolejne twierdzenie mówi o pochodnej funkcji odwrotnej.

  Twierdzenie

  Niech f będzie funkcją ciągłą i różnowartościową . Jeśli f jest różniczkowalna w punkcie x₀ oraz jej pochodna w tym punkcie jest różna od zera, to funkcja f ^-1 jest różniczkowalna w punkcie y₀ = f(x₀) przy czym ma miejsce następująca równość :

  (f -1) ' (y0) = 1/ f ' (x0).

  Na podstawie ostatniego twierdzenia i ze (znanych już !) wzorów na pochodne funkcji elementarnych nietrudno wyprowadzić następujące wzory:

  

  

  

  

  

  

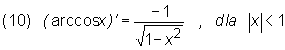
  Przydatny jest też wzór na pochodną logarytmiczną :

  Twierdzenie (pochodna logarytmiczna)

  Jeżeli funkcja f jest różniczkowalna na przedziale otwartym P, f(x) > 0 dla x ∈ P, to

  f' (x) = f(x)⋅ (ln f(x))'.

  Dowód. Wzór otrzymujemy obliczając pochodną funkcji ln f(x) ze wzoru na pochodną funkcji złożonej:

  (ln f(x))' = (1/f(x))⋅ f ' (x).

  Ostatnie twierdzenie najczęściej stosuje się do obliczania pochodnej funkcji postaci f(x)^g(x).

  Przykład

  Obliczmy pochodną funkcji f(x) = (sin x)^x .

  Mamy : f ' (x) = (sin x)^x [ln (sin x)^x]' = (sin x)^x[x ln (sin x)]' = (sin x)^x [ln(sin x) + x⋅ cosx⋅ (1/sinx)].

  Wykorzystany został wzór na pochodną iloczynu funkcji.

  
  

  ↔ poprzedni punkt