Dowód. Jeśli funkcja f jest stała w przedziale [a, b ], to f' (x) = 0 dla każdego x∈ (a,b), zatem w tym przypadku twierdzenie jest prawdziwe.

Załóżmy zatem, że funkcja f nie jest stała. Na mocy twierdzenia Weierstrassa z Wykładu III istnieją punkty c, c' ∈ [a, b] takie, że

Ponieważ funkcja f nie jest stała, to co najmniej jedna z nierówności:

jest prawdziwa. Załóżmy, że prawdziwa jest druga z tych nierówności (jeśli spełniona jest tylko pierwsza nierówność, to dowód jest bardzo podobny).

Ponieważ f(a) = f(b), to c∈ (a, b). Z wyboru punktu c wynika, że dla dowolnego h takiego, że c + h ∈ [a, b] mamy f(c+ h)- f(c) ≤ 0 czyli

Stąd, ponieważ f' (c) istnieje, otrzymujemy z twierdzenia o zachowywaniu nierówności z Wykładu III, że 0 ≤ f- ' (c) = f' (c) = f+ ' (c) ≤ 0, co implikuje, że f' (c) = 0.

Przykład

Niech f(x) = cos x, x ∈ [π ⁄ 2 , 3π / 2]. Funkcja ta spełnia założenia twierdzenia Rolle'a. Istnieje więc taki punkt c∈ [π ⁄ 2, 3π / 2], że f' (c)= 0. Nietrudno zauważyć, że c = π.

Spróbujmy twierdzenie Rolle'a zinterpretować geometrycznie. Rysunek poniższy przedstawia wykres funkcji spełniającej założenia twierdzenia Rolle'a:

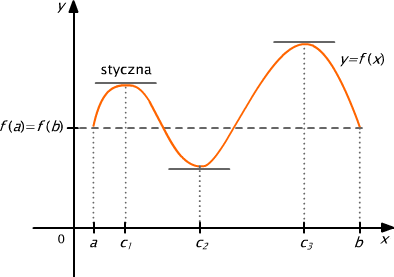
Rys. 5.1

Styczna do wykresu w punkcie a = (c₂, d) jest równoległa do osi Ox, co oznacza, że współczynnik kierunkowy stycznej jest równy 0 czyli f' (c₂) = 0.

Twierdzenie Lagrange'a orzeka fakt ogólniejszy niż Twierdzenie Rolle'a:

Jeśli funkcja f jest różniczkowalna w przedziale (a, b), to dla każdej siecznej wykresu funkcji istnieje równoległa do niej styczna. Stanie się to jasne, jeżeli weźmiemy pod uwagę fakt, że liczba (f(b)- f(a)) / (b- a) jest współczynnikiem kierunkowym prostej przechodzącej przez punkty (a, f(a)) oraz (b, f(b)), zaś f' (c) jest współczynnikiem kierunkowym pewnej stycznej do wykresu funkcji f. Ilustruje to rysunek:

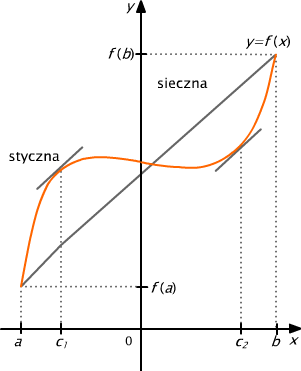
Rys. 5.2

Twierdzenie Lagrange'a jest też nazywane twierdzeniem o wartości średniej lub twierdzeniem o przyrostach.

Przykład

Stosując twierdzenie Lagrange'a udowodnimy nierówność

⎜ arctg b - arctg a⎥ ≤ ⎜ b-a⎥ dla a, b ∈ R.

Nierówność jest oczywista w przypadku gdy a=b. Udowodnimy ją w przypadku gdy a<b (przypadek a>b dowodzi się tak samo). Funkcja f(x) = arctg x spełnia założenia twierdzenia Lagrange'a w przedziale [a, b]. Przekształcając wzór z twierdzenia Lagrange'a możemy dla pewnej liczby c, a < c < b napisać

⎜ arctg b - arctg a⎥ = ⎜ b-a⎥ ⋅ ⎜ f '(c)⎥ = ⎜ b-a⎥ ⋅ (1/(1+c²)) ≤ ⎜ b-a⎥

ponieważ 1/ (1+c²) ≤ 1 dla c ∈ R.

Wnioski z twierdzenia Lagrange'a

1. Jeśli funkcja f jest ciągła w przedziale P oraz f' (x) = 0 dla dowolnego x∈ Int P, to funkcja f jest stała na P.
2. Jeśli funkcje f, g są różniczkowalne w przedziale (a, b) oraz f' (x) = g' (x) dla każdego x z tego przedziału, to istnieje liczba c taka, że

   f (x) = g(x) + c dla każdej liczby x ∈ (a, b).

3. Niech f, g będą funkcjami ciągłymi na przedziale P. Wówczas jeśli dla pewnej liczby x₀ z przedziału P spełnione są warunki:

   a) f (x₀) ≤ g(x₀)

   b) f' (x) ≤ g' (x) dla każdego x ∈ P, x > x₀, to f (x) ≤ g (x) dla każdego x ∈ P, x > x₀.

   Ponadto, jeśli którakolwiek z nierówności w założeniach (a), (b) jest ostra, to ostra jest też nierówność w tezie.

Przykłady

• Udowodnimy równość

arcsin x + arccos x = π / 2 dla x∈ [- 1, 1].

Rozpatrzmy funkcję f (x) = arcsin x + arccos x . Funkcja ta jest ciągła w przedziale [- 1, 1] oraz dla x∈ (- 1, 1) mamy:

zatem funkcja f jest stała na przedziale [- 1, 1]. Ponieważ f(0) = π / 2, to

• Udowodnimy nierówność

sin x < x dla x > 0.

Rozpatrzmy funkcje f (x) = sin x, g (x) = x, D_f = D_g = R. Przyjmujemy x₀ = 0 oraz P = [0, 1]. Oczywiście f(0) = g(0), f' (x) = cos x ≤ 1 = g' (x) dla x ∈ P, x > 0. Zatem na podstawie wniosku (3) otrzymujemy sin x ≤ x dla x > 0. Ponieważ dla 0 < x ≤ 1 prawdziwa jest nierówność f' (x) = cos x < 1 = g' (x), to dla 0 < x ≤ 1 mamy sin x < x. Dla x > 1 ostatnia nierówność jest oczywiście prawdziwa.