Definicja

Prostą x = a nazywamy asymptotą pionową lewostronną funkcji f jeśli

Zamieniając granice lewostronne na granice prawostronne dostajemy definicję asymptoty pionowej prawostronnej.

Prostą x = a nazywamy asymptotą pionową (obustronną) funkcji f jeśli jest ona asymptotą pionową lewostronną i prawostronną tej funkcji.

Uwaga

Funkcja ciągła może mieć asymptotę pionową jedynie w punktach, które nie należą do jej dziedziny i są końcami przedziałów, których sumą jest dziedzina funkcji.

Przykład

Ponieważ dziedziną funkcji y = tgx jest zbiór

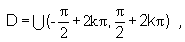
to asymptotami pionowymi tej funkcji mogą być jedynie proste

.

Ponieważ

,

to proste

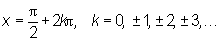
są asymptotami pionowymi obustronnymi funkcji tgx.

Podobnie sprawdza się, że proste

są asymptotami pionowymi obustronnymi funkcji tgx.

Definicja

Prostą y = ax + b nazywamy asymptotą ukośną funkcji f w ∞ wtedy i tylko wtedy, gdy

.

Prostą y = ax + b nazywamy asymptotą ukośną funkcji f w − ∞ wtedy i tylko wtedy, gdy

.

Jeśli współczynnik kierunkowy a asymptoty ukośnej jest równy 0, to mówimy, że prosta y = b jest asymptotą poziomą.

Wprost z definicji wynika następująca

Uwaga

Prosta y = b jest asymptotą poziomą funkcji f w ∞ wtedy i tylko wtedy, gdy. Tak samo jest w − ∞ .

Przykład

Znajdźmy asymptoty funkcji zadanej wzorem:

Ponieważ dziedziną funkcji f jest R, to funkcja ta nie ma asymptot pionowych. Policzmy:

.

Stąd wynika, że prosta y = 1/5 jest asymptotą poziomą rozpatrywanej funkcji w ∞, zaś prosta y = 1/4 jest jej asymptotą poziomą w − ∞.

Kolejne twierdzenie podaje praktyczny sposób na znajdowanie asymptot ukośnych (i poziomych) danej funkcji.

Twierdzenie

Prosta y = ax + b jest asymptotą ukośną funkcji f w ∞ wtedy i tylko wtedy, gdy

Ponadto: jeśli którakolwiek z granic nie istnieje lub jest niewłaściwa, to f nie ma asymptoty ukośnej w ∞.

Analogicznie charakteryzuje się asymptoty ukośne w − ∞.

Twierdzenie

Prosta y = ax + b jest asymptotą ukośną funkcji f w − ∞ wtedy i tylko wtedy, gdy

Ponadto: jeśli którakolwiek z granic nie istnieje lub jest niewłaściwa, to f nie ma asymptoty ukośnej w − ∞.

Wniosek

Każda funkcja ma co najwyżej jedną asymptotę ukośną w ∞ i co najwyżej jedną asymptotę ukośną w − ∞. W szczególności: gdy istnieje właściwa granica

to funkcja ma asymptotę poziomą i jest to jedyna asymptota ukośna danej funkcji, nie ma więc potrzeby liczenia granic występujących w ostatnich twierdzeniu, bo otrzymalibyśmy a = 0. Ta sama uwaga dotyczy asymptot w ∞.

Przykład

Wyznaczmy asymptoty funkcji f(x) = x⁴/ (1+x)³ .

Dziedziną tej funkcji jest zbiór (− ∞, − 1)∪ (− 1, ∞ ). Zatem prosta x = -1 może być asymptotą pionową danej funkcji.

Obliczamy:

zatem prosta x = -1 rzeczywiście jest (obustronną) asymptotą funkcji f.

Sprawdźmy czy f ma asymptoty ukośne. Obliczmy odpowiednie granice.

czyli a = 1.

Następnie

.

Z powyższych obliczeń wynika, że prosta y = x - 3 jest asymptotą ukośną f w ∞.

Bardzo podobne obliczenia wykazują, że ta sama prosta jest asymptotą ukośną f w -∞.