Definicja

Powiemy, że funkcja f jest wypukła w przedziale P, jeśli dla dowolnych liczb x₁ , x₂∈ P i dla każdej liczby λ , 0 < λ < 1 spełniony jest warunek:

f( λ x₁ + (1-λ )x₂) ≤ λ f( x₁) + ( 1-λ ) f(x₂).

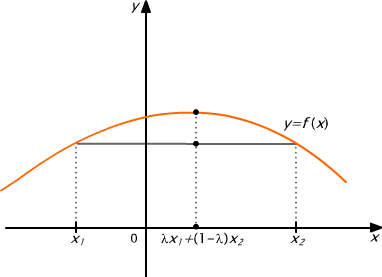
Używając języka geometrii możemy powiedzieć, że funkcja f jest wypukła, jeżeli każdy punkt odcinka siecznej wykresu leży ponad wykresem lub na wykresie.

Definicja

Powiemy, że funkcja jest ściśle wypukła w przedziale P jeśli dla dowolnych różnych liczb x₁ , x₂ ∈ P i dla każdej liczby λ , 0 < λ < 1 spełniony jest warunek:

f( λ x₁ + (1-λ )x₂)
< λ f( x₁) + ( 1-λ ) f(x₂).

Geometrycznie: Każdy punkt wnętrza odcinka siecznej łączącej punkty (x₁, f(x₁)) oraz (x₂, f(x₂)) leży ponad wykresem funkcji f .

Ilustrację geometryczną funkcji wypukłej, która nie jest ściśle wypukła podana jest na Rys. 6.1, zaś funkcji ściśle wypukłej na Rys. 6.2.

Zamieniając w obu powyższych definicjach nierówności na przeciwne otrzymamy definicje funkcji wklęsłej i ściśle wklęsłej:

Definicja

Powiemy, że funkcja f jest wklęsła w przedziale P, jeśli dla dowolnych liczb x₁, x₂ ∈ P i dla każdej liczby λ , 0 < λ < 1 spełniony jest warunek:

f( λ x₁ + (1-λ )x₂) ≥ λ f( x₁) + ( 1-λ ) f(x₂).

Używając języka geometrii możemy powiedzieć, że funkcja f jest wklęsła, jeżeli każdy punkt odcinka siecznej wykresu leży pod wykresem lub na wykresie.

Definicja

Powiemy, że funkcja jest ściśle wklęsła w przedziale P jeśli dla dowolnych różnych liczb x₁ , x₂ ∈ P i dla każdej liczby λ , 0 < λ < 1 spełniony jest warunek:

f( λ x₁ + (1-λ )x₂) > λ f( x₁) + ( 1-λ ) f(x₂).

Geometrycznie: Każdy punkt wnętrza odcinka siecznej łączącej punkty (x₁, f(x₁)) oraz (x₂, f(x₂)) leży pod wykresem funkcji f.

Ilustrację geometryczną funkcji wklęsłej, która nie jest ściśle wwlęsła podana jest na Rys. 6.3, zaś funkcji ściśle wklęsłej na Rys. 6.4 .

Twierdzenie

Niech funkcja f będzie funkcją ciągłą w przedziale P , różniczkowalną we wnętrzu P. Wówczas

funkcja f jest wypukła w przedziale P wtedy i tylko wtedy, gdy jej pochodna f′ jest funkcją niemalejącą w Int P;
funkcja f jest ściśle wypukła w przedziale P wtedy i tylko wtedy, gdy jej pochodna f′ jest funkcją rosnącą w Int P;
funkcja f jest wklęsła w przedziale P wtedy i tylko wtedy, gdy jej pochodna f′ jest funkcją nierosnącą w Int P ;
funkcja f jest ściśle wklęsła w przedziale P wtedy i tylko wtedy, gdy jej pochodna f′ jest funkcją malejącą w Int P.

Twierdzenie

Załóżmy, że funkcja f jest ciągła w przedziale P oraz dwukrotnie różniczkowalna w Int P. Wówczas

funkcja f jest wypukła w przedziale P wtedy i tylko wtedy, gdy f′ ′ (x) ≥ 0 dla każdego x ∈ Int P;
funkcja f jest ściśle wypukła w przedziale P wtedy i tylko wtedy, gdy f′ ′ (x) ≥ 0 dla każdego x ∈ Int P oraz f′ ′ nie jest funkcją zerową na żadnym podprzedziale przedziału P niezerowej długości;
funkcja f jest wklęsła w przedziale P wtedy i tylko wtedy, gdy f′ ′ (x) ≤ 0 dla każdego x ∈ Int P;
funkcja f jest ściśle wklęsła w przedziale P wtedy i tylko wtedy, gdy f′ ′ (x) ≤ 0 dla każdego x ∈ Int P oraz f′ ′ nie jest funkcją zerową na żadnym podprzedziale przedziału P niezerowej długości.

• Jeśli f′ ′ (x) > 0 dla każdego x ∈ (a, b), to funkcja f jest ściśle wypukła w przedziale (a, b). Jeśli ponadto f jest ciągła w [a, b] , to jest też wypukła w przedziale [a, b].

• Jeśli f′ ′ (x) < 0 dla każdego x ∈ (a, b), to funkcja f jest ściśle wklęsła w przedziale (a, b). Jeśli ponadto f jest ciągła w [a, b], to jest też ściśle wklęsła w przedziale [a, b].

Sformułujemy jeszcze jedną definicję związaną z wypukłością i wklęsłością funkcji.

Definicja

Załóżmy, że funkcja f jest określona na pewnym otoczeniu punktu x₀. Powiemy, że punkt (x₀, f(x₀)) jest punktem przegięcia (w skrócie p.p.) funkcji, jeżeli istnieje liczba δ > 0 taka, że na jednym z przedziałów (x_0,x₀+ δ ), (x₀- δ, x₀) funkcja f jest ściśle wypukła, zaś na drugim ściśle wklęsła.

Zamiast mówić: punkt (x₀ , f(x₀)) jest punktem przegięcia funkcji f mówi się często: x₀ jest punktem przegięcia f.

Twierdzenie

Załóżmy, że funkcja f jest ciągła w pewnym otoczeniu punktu x₀. Wówczas:

jeśli x₀ jest punktem przegięcia funkcji f, to f′ ′ (x₀) = 0 lub f′ ′ (x₀) nie istnieje.
jeśli f′ ′ (x) zmienia znak przy przejściu przez punkt x₀ , to x₀ jest punktem przegięcia funkcji f.
jeśli f′ (x₀) = f′ ′ (x₀) = ...= f ^(n-1)(x₀) = 0 oraz f ⁽ⁿ⁾(x₀) ≠ 0 i funkcja f ⁽ⁿ⁾ jest ciągła w punkcie x₀, to
(a) gdy n jest liczbą nieparzystą to x₀ jest punktem przegięcia funkcji f;

(b) gdy n jest liczbą parzystą to x₀ nie jest punktem przegięcia funkcji f.

Dziedziną funkcji f jest zbiór R. Funkcja f posiada pochodne dowolnego rzędu w całej swojej dziedzinie. Policzmy drugą pochodną funkcji f:

Miejsca zerowe i znak drugiej pochodnej funkcji f są takie jak miejsca zerowe i znak trójmianu 2x² - 1, ponieważ funkcja wykładnicza przyjmuje wartości dodatnie.

funkcja f ′′ zmienia znak. Są to w takim razie punkty przegięcia funkcji f. Ponadto

Na podstawie sformułowanych wyżej twierdzeń możemy ostatecznie stwierdzić, że f jest funkcją ściśle wypukłą w przedziale

oraz w przedziale

, f jest funkcją ściśle wklęsłą w przedziale