Definicja
Jeśli funkcja f ma w punkcie x0 pochodną rzędu k , to wielomianem Taylora rzędu k funkcji f w xo nazywamy wielomian
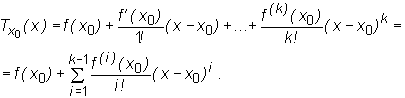
W szczególnym przypadku gdy x0 =0 wielomian
![]()
| następny punkt ≈ |
Definicja
Jeśli funkcja f ma w punkcie x0 pochodną rzędu k , to wielomianem Taylora rzędu k funkcji f w xo nazywamy wielomian
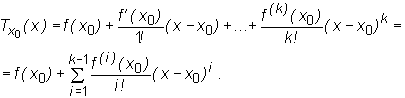
W szczególnym przypadku gdy x0 =0 wielomian
![]()
Uwagi
• Z definicji wielomianu Taylora rzędu k funkcji f w punkcie xo wynika, że stopień tego wielomianu wynosi co najwyżej k, ale może być mniejszy niż k (gdy f(k)(x0)=0).
• Łatwo widać, że wielomian Taylora rzędu k funkcji f w xo , to jedyny wielomian stopnia niewiększego niż k taki, że
![]()
Wynika stąd, że gdy f jest wielomianem stopnia n ≤ k to wielomianem Taylora funkcji f w x0 jest właśnie funkcja f (jeśli n > k to f nie jest swoim wielomianem Taylora rzędu k).
Okazuje się, że dla x bliskich x0 liczba ![]() jest dobrym przybliżeniem liczby f(x). Dokładniej oszacować wielkość błędu Rn(x) tego przybliżenia pozwala poniższe twierdzenie.
jest dobrym przybliżeniem liczby f(x). Dokładniej oszacować wielkość błędu Rn(x) tego przybliżenia pozwala poniższe twierdzenie.
Twierdzenie (Wzór Taylora z resztą w postaci Lagrange'a)
Jeśli funkcja f
(1) ma ciągłą pochodną rzędu n-1 w przedziale [x0, x]
(2) ma pochodną rzędu n w przedziale otwartym (x0, x)
to istnieje punkt c ∈ (x0, x) taki, że
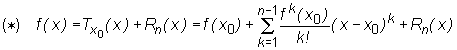
![]()
zaś Tx0(x) jest wielomianem Taylora rzędu n -1.
Wzór (∗) nazywamy wzorem Taylora z n-tą resztą w postaci Lagrange'a, a samo wyrażenie
![]()
nazywamy n-tą resztą w postaci Lagrange'a
Uwagi
• Wzór Taylora pozostaje słuszny dla przedziału [x, x0] ( wtedy x0 ∈ (x, x0) ).
W obu przypadkach: x0 > x, x0 < x resztę można zapisać jednym wzorem
![]()
• Dla x0=0 wzór Taylora przybiera postać
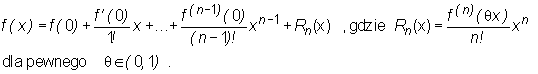
i jest nazywany wzorem MacLaurina z n-tą resztą.
• Pomijając we wzorze Taylora resztę Rn(x) otrzymujemy w otoczeniu punktu x0 przybliżenie funkcji f wielomianem stopnia (co najwyżej) n-1:
![]()
czyli
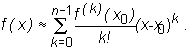
Zauważmy, że n-ta reszta z wzoru Taylora to po prostu liczba
![]()
czyli błąd przybliżenia liczby f(x) liczbą ![]()
Przez oszacowaniu błędu takiego przybliżenia rozumiemy wyznaczenie liczby a takiej, że ⏐ Rn(x)⏐ ≤ a.
Przykłady
• Wypiszemy wzór MacLaurina z 4-tą resztą R4(x) dla funkcji f(x)=cosx i oszacujemy błąd przybliżenia funkcji f wielomianem MacLaurina rzędu 3 gdy ⎪x⎪≤0,3.
Ponieważ f(x)=cosx, f'(x)=-sinx, f''(x)=-cosx, f(3)(x)=sinx, f(4)(x)=cosx,
f(0)=1, f'(0)=0, f''(0)=-1, f(3)(0)=0, to wzór MacLaurina z R4(x) dla funkcji cosx ma postać
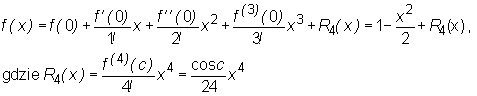
dla pewnego c leżącego między 0 oraz x. Zatem wielomian MacLaurina rzędu 3 dla funkcji f(x)=cosx ma postać
![]()
i w tym przypadku stopień wielomianu MacLaurina jest niższy niż jego rząd. Pozostaje jeszcze oszacować błąd przybliżenia cosx przez ![]() gdy ⎪
x⎪
≤
0,3. Otóż
gdy ⎪
x⎪
≤
0,3. Otóż

Przedostatnia nierówność wynika z tego, że ⎪ cosc⎪≤ 1.
• Wypiszemy wzór Taylora z 4-tą resztą dla funkcji f(x)=x/(x-3) w punkcie x0=-2. Podamy wzór przybliżony na wartości tej funkcji jaki otrzymujemy odrzucając po prawej stronie wzoru Taylora resztę R4(x) i oszacujemy błąd jaki popełniamy stosując ten wzór w punkcie -1,95 tj. przybliżając liczbę f(-1,95) przez T-2(-1,95), gdzie T-2(x) jest wielomianem Taylora rzędu 3 funkcji f.
![]()
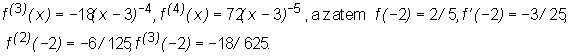
Wynika stąd, że wzór Taylora z R4(x) dla funkcji f w punkcie x0 jest postaci
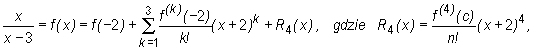
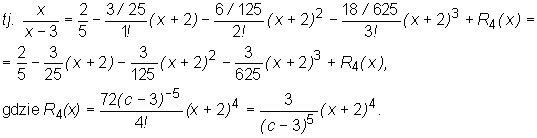
dla pewnego c leżącego między -2 oraz x.
W szczególności wielomian Taylora rzędu 3 dla funkcji f w punkcie -2 ma postać

a zatem przybliżony wzór na wartości funkcji f dla x bliskich -2 ma postać
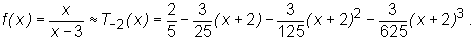
W szczególności:
![]()
Błąd tego przybliżenia możemy oszacować w następujący sposób:
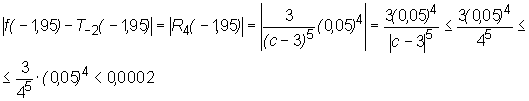
ponieważ dla c takiego, że -2<c<-1,95 mamy ⎜ c− 3⎥ ∈ (4,95, 5), a zatem 4<⎜ c− 3⎥ skąd ⎜ c− 3⎥ − 5≤ 1/45.
• Wypiszemy wzór Taylora z 3-tą resztą dla funkcji f(x) = x1/3 w punkcie x0=125 i zastosujemy go do obliczenia w przybliżeniu liczby 1241/3 i oszacowania błędu tego przybliżenia.
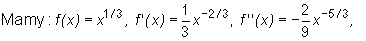
![]()
Wynika stąd, że wzór Taylora z R3(x) dla funkcji f w punkcie x0=125 jest postaci
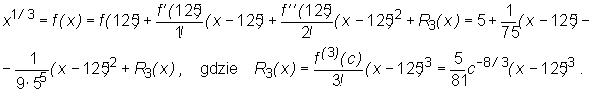
dla pewnego c leżącego między 125 oraz x.
W szczególności wielomian Taylora rzędu 2 dla funkcji f w punkcie 125 ma postać
![]()
a zatem przybliżony wzór na wartości funkcji f dla x bliskich 125 ma postać
![]()
W szczególności weźmy x = 124. Mamy wtedy:
![]()
Błąd tego przybliżenia możemy oszacować w następujący sposób:
![]()
Ostatnia nierówność wynika z tego, że 124<c<125 a zatem 4<1241/3<c1/3 co implikuje, że
c-8/3<4-8.
• Wyznaczymy teraz wielomiany MacLaurina rzędu 3 i 4 oraz wzór Taylora z R5(x) punkcie -1 dla funkcji f(x)=x4-x3+3x2+1.
Mamy f′ (x)=4x3-3x2+6x, f′ ′ (x)=12x2-6x+6, f(3)(x)=24x-6, f(4)(x)=24, f(5)(x)=0, zatem f(0)=1, f′ (0)=0, f′ ′ (0)=6, f(3)(0)=-6, f(4)(0)=24. Otrzymujemy zatem wielomian MacLaurina rzędu 3:
![]()
i wielomian MacLaurina rzędu 4:
![]()
Ostatnia równość ilustruje uwagę z początku wykładu mówiącą o tym, że jeśli funkcja f jest wielomianem stopnia n to każdy jej wielomian Taylora rzędu k≥ n jest jej równy.
Aby wyznaczyć wzór Taylora z R5(x) dla funkcji f(x) w punkcie x0=1 wyliczamy:
f(1)=4, f′ (1)=7, f′ ′ (1)=12, f(3)(1)=18, f(4)(1)=24 , co daje
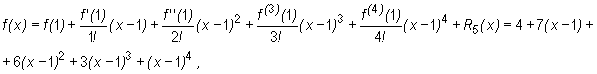
ponieważ (zgodnie z uwagą z początku wykładu) R5(x)=0, gdyż f(5)(x)=0. W szczególności oznacza to, że zapisaliśmy wielomian f jako kombinację liniową potęg jednomianu x-1.
Uwaga
Podobnie wypisując dla dowolnego wielomianu f stopnia n≤ k wzór Taylora z Rk(x) w dowolnym punkcie x0 wyznaczamy po prostu zapis tego wielomianu jako sumy potęg jednomianu x-x0.
• Wypiszemy wzór MacLaurina z n-tą resztą dla funkcji f(x) = ex. Oszacujemy błąd tego przybliżenia liczby e = f(1) przez liczbę T0(1), gdzie T0(x) jest wielomianem Taylora rzędu n-1 funkcji ex.
Mamy: f(x) = ex, f′ (x) = ex, f′ ′ (x) = ex, ..., f(n-1)(x) = ex, f(n)(x) = ex, czyli
f(0) = 1, f′ (0) = 1, f′ ′ (0) = 1, ..., f(n-1)(0) = 1. Zatem wzór MacLaurina z n-tą resztą dla funkcji ex wygląda następująco:
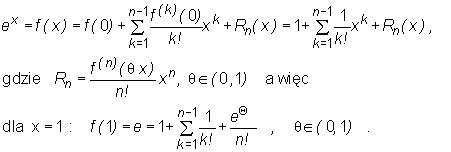
Oszacujmy teraz błąd przybliżenia liczby e przez liczbę
![]() :
: 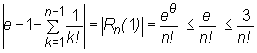 .
.
W szczególności dla n = 5 błąd nie przekracza 1/40 , a dla n = 7 nie przekracza 1/1680.
Uwaga
• Istnieją również inne wzory opisujące n-tą resztę Rn(x). Na przykład wiadomo, że jeśli spełnione są założenia twierdzenia o wzorze Taylora z resztą w postaci Lagrange'a to dla każdego x∈ (a, b), istnieje λ ∈ (0,1) takie, że
![]()
To ostatnie wyrażenie nazywamy n-tą resztą w postaci Cauchy'ego. Reszta w postaci Lagrange'a i reszta w postaci Cauchy'ego to różne wzory na tę samą liczbę
![]()
Użycie reszty w postaci Lagrange'a pozwala na znacznie prostsze (choć często dużo słabsze) oszacowanie błędu przybliżenia Rn(x) niż użycie reszty w postaci Cauchy'ego. Z tego powodu używaliśmy tu tylko reszty w postaci Lagrange'a.
| następny punkt ≈ |