Definicja (szereg Taylora funkcji)
Jeśli funkcja f ma w punkcie x0 pochodne dowolnego rzędu, to szeregiem Taylora funkcji f w punkcie x0 nazywamy wyrażenie
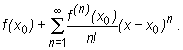
| ↔ poprzedni punkt | następny punkt ≈ |
Definicja (szereg Taylora funkcji)
Jeśli funkcja f ma w punkcie x0 pochodne dowolnego rzędu, to szeregiem Taylora funkcji f w punkcie x0 nazywamy wyrażenie
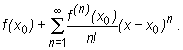
Dla ujednolicenia zapisu przyjmuje się oznaczenie f(0)(x) = f(x) i wtedy szereg Taylora możemy zapisać w postaci
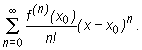
Definicja
Szeregiem MacLaurina funkcji f nazywamy szereg Taylora f w punkcie
X0 = 0 czyli wyrażenie postaci
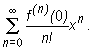
Definicja
Niech − ∞ ≤ a < b ≤ ∞. Jeśli funkcja f ma w każdym punkcie x∈ ( a, b) pochodną dowolnego rzędu, to mówimy, że f jest klasy C∞ w przedziale ( a, b).
Można udowodnić następujące:
Twierdzenie (o jednoznaczności rozwinięcia w szereg potęgowy)
Niech x0∈ ( a, b) i niech f będzie funkcją o wartościach rzeczywistych określoną na ( a, b). Jeśli istnieje ciąg ( cn) liczb rzeczywistych taki, że
![]()
• funkcja f jest klasy C∞ w ( a,b),
![]()
![]()
Twierdzenie o jednoznaczności rozwinięcia funkcji w szereg potęgowy pozwala czasem wyznaczyć rozwinięcie funkcji w jej szereg Taylora bez wyznaczania pochodnych.
Przykłady
•
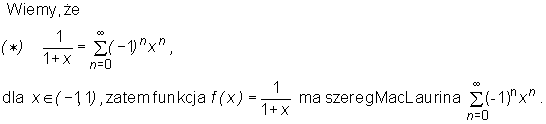
• Ponieważ x2∈ (-1, 1) dla x∈ (-1, 1), to z równości
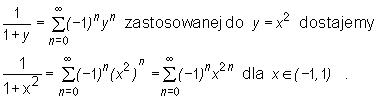
Zatem z twierdzenia o jednoznaczności rozwinięcia funkcji w szereg potęgowy wynika, że funkcja
![]()
•
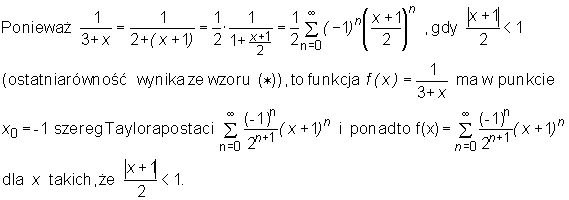
Uwaga
Może się niestety zdarzyć tak, że funkcja f jest klasy C∞ w pewnym otoczeniu punktu x0 ale
• albo szereg Taylora funkcji f jest zbieżny tylko w punkcie x0,
• albo szereg Taylora funkcji f jest co prawda zbieżny w pewnym sąsiedztwie punktu x0 , ale jego suma ma niewiele wspólnego z funkcją f .
Na przykład można pokazać, że funkcja
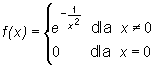
![]()
jest klasy C∞ na R i spełnia warunek f(n)(0) = 0 dla n = 0, 1, 2, ... czyli szeregiem MacLaurina tej funkcji jest szereg
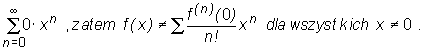
Twierdzenie (o rozwijaniu funkcji w szereg Taylora)
Załóżmy, że w pewnym otwartym przedziale (a, b) zawierającym x0 funkcja f jest klasy C∞. Jeśli dla każdego x∈ (a, b) zachodzi równość
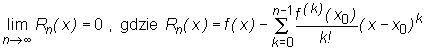
jest n-tą resztą we wzorze Taylora dla funkcji f w punkcie x0, to
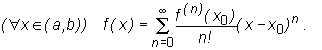
Dowód. Z definicji sumy szeregu wynika, że
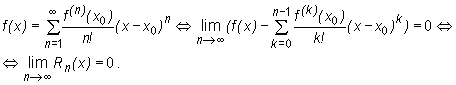
Korzystać będziemy z następującego faktu
Uwaga
Dla każdego x ∈ R
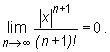
Dowód. Ustalamy x ≠ 0 i rozpatrujemy pomocniczy szereg liczbowy
Poniżej podajemy szeregi MacLaurina pewnych funkcji elementarnych.
![]()
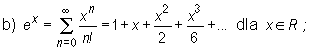
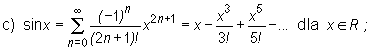
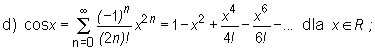
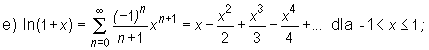
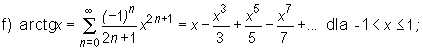
![]()
Dla przykładu zostanie przedstawiony szkic dowodu punktu b).
Z obliczeń wykonanych przy wyznaczaniu wielomianu MacLaurina dla funkcji f(x)=ex wynika, że ex ma szereg MacLaurina
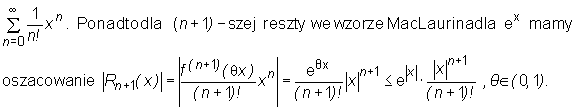
Ostatnia nierówność wynika z tego, że θ x ≤ ⎜θ x⎥ ≤ ⎢x⎥, zaś funkcja f(x)=ex jest dodatnia i rosnąca w R.

Z twierdzenia o rozwijaniu funkcji w szereg Taylora wnioskujemy, że
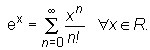
Korzystając ze znanych rozwinięć funkcji w szeregi Maclaurina i z twierdzenia o jednoznaczności rozwinięcia funkcji w szereg potęgowy można wyznaczać rozwinięcia pewnych funkcji w szeregi Taylora.
Przykłady
Stosując znane rozwinięcia funkcji w szereg Maclaurina wyznaczymy szereg Taylora podanej funkcji f w punkcie x0 i wskażemy przedział na którym funkcja jest równa sumie swojego szeregu Taylora (nie badając co się dzieje poza tym przedziałem).
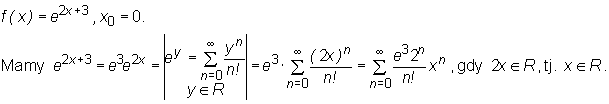

i jest równa jego sumie na R.
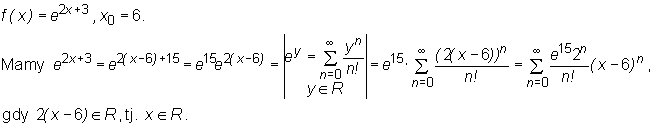
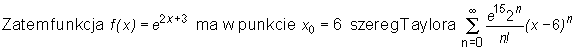
i jest równa jego sumie na R.
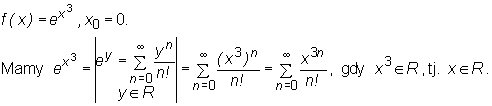
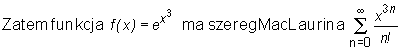
i jest równa jego sumie na R.
f(x) = ln(10+3x), x0 = 0.
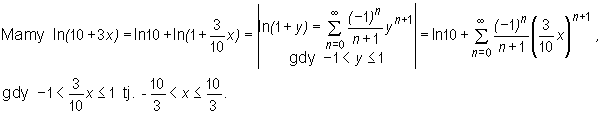
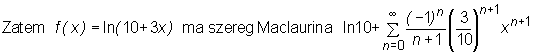
i jest równa jego sumie w przedziale (− 10/ 3, 10/ 3].
f(x) = ln(10+3x), x0 = 1.
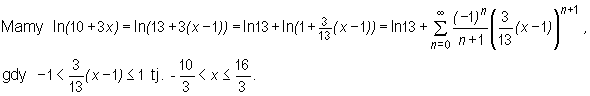

i jest równa jego sumie w przedziale (− 10/ 3, 16/ 3].
| ↔ poprzedni punkt | następny punkt ≈ |