Definicja
Całką nieoznaczoną funkcji f na przedziale (a, b) nazywamy zbiór wszystkich funkcji pierwotnych funkcji f i oznaczamy symbolem
| następny punkt ≈ |
Niech f będzie funkcją określoną na przedziale (a, b).
Definicja
Funkcję różniczkowalną F określoną na (a, b), spełniającą warunek
F '(x) = f (x), dla każdego x ∈ (a, b) |
| Wyznaczanie funkcji pierwotnej jest więc operacją odwrotną do różniczkowania funkcji |
Uwaga
W podanej definicji przedział otwarty można zastąpić przedziałem domkniętym. Wówczas różniczkowalność funkcji F w przedziale [a, b] oznacza istnienie jej pochodnej w przedziale otwartym (a, b) oraz istnienie pochodnych jednostronnych F'+(a) i F'-(b) na krańcach przedziału.
Ponieważ pochodna funkcji stałej jest równa 0, z powyższej definicji wynika, że funkcja pierwotna nie jest określona w sposób jednoznaczny. Jeśli bowiem F jest funkcją pierwotną funkcji f, to również funkcja F + C, gdzie C oznacza dowolną stałą, jest jej funkcją pierwotną. Z drugiej strony, jeśli F i G są dwiema dowolnymi funkcjami pierwotnymi funkcji f, to z własności pochodnej mamy
| (F(x) - G(x)) ' = F '(x) - G '(x) = f(x) - f(x) = 0. |
| Stąd F(x) - G(x) = C, czyli G(x) = F(x) + C. |
Udowodniliśmy w ten sposób następujące twierdzenie:
Twierdzenie
Jeżeli F jest funkcją pierwotną funkcji f na przedziale (a, b), to każda funkcja pierwotna określona jest wzorem
G(x) = F(x) + C, gdzie C jest stałą. |
Przykład
Bezpośrednio z definicji wynika, że funkcją pierwotną funkcji f(x) = 2x jest funkcja F(x) = x2, ponieważ (x2)' = 2x. Każdą inną funkcję pierwotną możemy wyznaczyć z wzoru G(x) = x2 + C, przez odpowiedni dobór stałej C.
Definicja
Całką nieoznaczoną funkcji f na przedziale (a, b) nazywamy zbiór wszystkich funkcji pierwotnych funkcji f i oznaczamy symbolem
Symbol ten czytamy następująco: "całka f od x (po) dx".
Jeżeli F jest dowolną, ustaloną funkcją pierwotną funkcji f, to przyjmuje się następującą konwencję zapisu:
Stałą C nazywamy stałą całkowania.
Przykłady
![]()
![]()
Uwaga

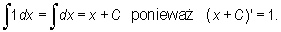
Definicja
Funkcję, dla której na danym przedziale istnieje całka nieoznaczona, nazywamy całkowalną w sensie Newtona ( lub krócej całkowalną ) na tym przedziale.
Przykład funkcji f(x) = sgn x pokazuje, że istnieją funkcje nie posiadające funkcji pierwotnej.
ι Pytanie kontrolne 8.1
Wykaż, ze funkcja f(x) = sgn x nie ma funkcji pierwotnej.
Zobacz odpowiedźPowstaje więc pytanie:
Dla jakich funkcji istnieje całka nieoznaczona?
Częściową odpowiedź na nie daje poniższe, ważne twierdzenie.
Twierdzenie
Jeżeli funkcja f jest ciągła na przedziale (a, b), to jest na tym przedziale całkowalna.
Ciągłość funkcji jest zatem warunkiem wystarczającym jej całkowalności. Nie jest natomiast warunkiem koniecznym tzn. istnieją funkcje całkowalne, które nie są ciągłe. Przykładem jest funkcja
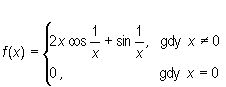
ι Pytanie kontrolne 8.2
Udowodnij, że powyższa funkcja jest nieciągła w punkcie x = 0, lecz całkowalna w R.
Zobacz odpowiedźKlasa funkcji ciągłych jest jednak na tyle liczna, że zaspokaja potrzeby większości zastosowań (w szczególności wszystkie funkcje elementarne są ciągłe), a ponadto warunek ciągłości jest stosunkowo łatwo weryfikowalny.
Wyznaczanie całek nieoznaczonych nie jest proste. Na ogół jest zadaniem znacznie trudniejszym niż różniczkowanie. Co więcej, istnieją funkcje ciągłe (w tym funkcje o dużym znaczeniu praktycznym), których funkcje pierwotne nie dadzą się wyrazić za pomocą funkcji elementarnych. Należą do nich np.
![]() .
.
O takich funkcjach mówimy, że nie są całkowalne elementarnie.
Bezpośrednio z definicji oraz znanych wzorów na pochodne funkcji wynikają tzw. wzory podstawowe prezentowane w poniższej tablicy.
Tablica 8.1 Podstawowe wzory rachunku całkowego
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Przykłady
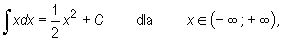
![]()
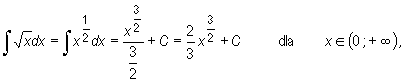
![]()
Za pomocą wzorów podstawowych można wyznaczyć tylko nieliczne całki nieoznaczone. Obliczanie innych całek umożliwiają stosowne twierdzenia.
| następny punkt ≈ |