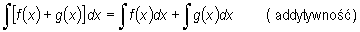Twierdzenie (o liniowości całki nieoznaczonej)

Jeżeli funkcje f i g są całkowalne na pewnym przedziale P, to funkcje f + g oraz A f , gdzie A oznacza dowolną stałą, są także całkowalne na tym przedziale, przy czym

"całka sumy równa się sumie całek",

"stałą można wynieść/wyłączyć przed znak całki".

Dowód

Dowód twierdzenia wynika bezpośrednio z liniowości operacji różniczkowania. Niech F oznacza funkcję pierwotną dla funkcji f, zaś G - funkcję pierwotną dla g. Wtedy

Stąd wynika pierwszy wzór.

Ponadto

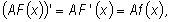
co uzasadnia wzór drugi i kończy dowód.

Własność liniowości odgrywa istotną rolę w technice wyznaczania całek, ponieważ umożliwia sprowadzenie obliczania całek kombinacji liniowych funkcji do obliczania całek poszczególnych składników.

Przykłady

• 

  (W analogiczny sposób wyznaczamy całkę nieoznaczoną dowolnego wielomianu.)

• 

W pewnych przypadkach, przed zastosowaniem twierdzenia, należy odpowiednio przekształcić funkcję podcałkową.

Uwagi

• Stałą całkowania C dopisujemy dopiero na końcu, po znalezieniu konkretnej funkcji pierwotnej. Dopóki po prawej stronie znaku równości występuje co najmniej jedna całka nieoznaczona, dopisywanie stałej całkowania jest zbędne; tkwi ona wówczas ukryta w symbolu całki nieoznaczonej, zgodnie z sensem tego symbolu.
• Przy obliczaniu całek nieoznaczonych zazwyczaj nie wskazujemy wyraźnie przedziałów, do których te obliczenia się odnoszą, zakładając poprawność wykonywanych w ich obrębie działań.
• Poprawność obliczenia całki nieoznaczonej możemy zawsze sprawdzić różniczkując otrzymaną funkcję. Wynikiem różniczkowania musi być funkcja podcałkowa.