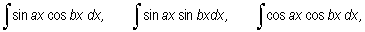
| ↔ poprzedni punkt | następny punkt ≈ |
Funkcje trygonometryczne całkujemy przekształcając funkcję podcałkową za pomocą odpowiednich tożsamości trygonometrycznych oraz wykorzystując podstawienia, które sprowadzają zadanie do całkowania pewnej funkcji wymiernej. Podamy teraz metody całkowania różnych typów całek funkcji trygonometrycznych.
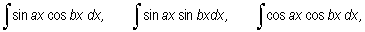 |
wyznaczamy korzystając z tożsamości trygonometrycznych, które iloczyn funkcji trygonometrycznych zamieniają na sumę, lub różnicę
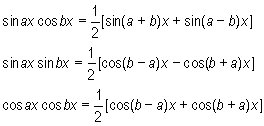 |
Przykład
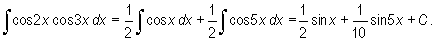
wyznaczamy
![]()
bądź wzory rekurencyjne, lub podstawienie t = tg x, gdy n i m są parzyste.
Przykłady
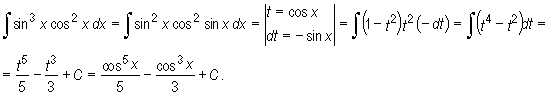
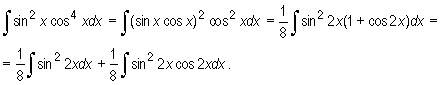
Wyznaczamy obie całki
![]()
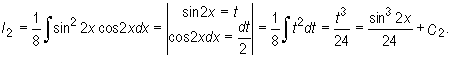
Ostatecznie otrzymujemy
![]()
gdzie R oznacza funkcję wymierną względem wymienionych argumentów, wyznaczamy stosując podstawienie
Wówczas
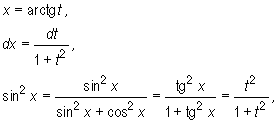
![]()
![]()
Po zastosowaniu powyższego podstawienia otrzymujemy całkę funkcji wymiernej.
Przykład
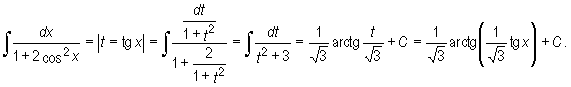
wyznaczamy stosując podstawienie:
Stąd
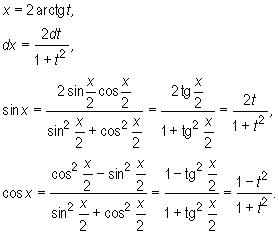
Podstawienie to sprowadza zadanie do wyznaczenia całki pewnej funkcji wymiernej.
Przykład
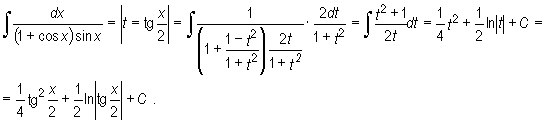
Uwaga
Powyższe podstawienie, zwane podstawieniem uniwersalnym, umożliwia również wyznaczenie całek funkcji trygonometrycznych rozważanych wcześniej typów, niemniej prezentowane tam metody będą na ogół znacznie efektywniejsze obliczeniowo.
| ↔ poprzedni punkt | następny punkt ≈ |