| ↔ poprzedni punkt | następny punkt ≈ |
Omawianie całkowania funkcji zawierających wyrażenia niewymierne (pierwiastkowe) ograniczymy do przypadków mających największe znaczenie praktyczne.
Całkowanie funkcji zawierających pierwiastek z wyrażenia liniowego
Całkę
gdzieR oznacza funkcję wymierną dwóch argumentów, sprowadzamy do całki funkcji wymiernej przez podstawienie
Przykład
Obliczymy całkę

Całkowanie funkcji zawierających pierwiastek kwadratowy trójmianu kwadratowego
Można wykazać, że całka postaci
gdzie R oznacza funkcję wymierną dwóch argumentów, da się wyrazić za pomocą funkcji elementarnych. Efektywna metoda jej wyznaczania polega na sprowadzeniu zadania do obliczenia jednej z całek typu
Pierwsza z nich należy do kategorii całek podstawowych
Drugą, przy założeniu x 2 + k > 0, wyznaczymy sprowadzając do całki funkcji wymiernej przez tzw. podstawienie Eulera
Mamy
Stąd
 |
Zatem
Ostatecznie
Przykład
Obliczymy całkę
![]()
Sprowadzamy trójmian do postaci kanonicznej
![]()
Za pomocą podstawienia t = x - 3 dostajemy całkę omawianego typu

Jeżeli współczynnik przy najwyższej potędze trójmianu jest ujemny (a < 0), to w analogiczny sposób całkę
sprowadzamy do całki typu pierwszego.
W celu obliczenia całki
przedstawiamy jąw postaci
 |
Pierwszą całkę wyznaczamy metodą całkowania przez części
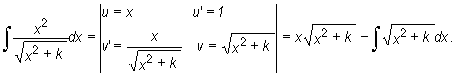 |
Ponieważ drugą całkę wyznaczyliśmy wcześniej, po podstawieniu wyników do wzoru dostajemy
Stąd ostatecznie
Analogicznie postępując można wyznaczyć również całkę
Prościej jest jednak zastosować podstawienie x = sint.

ι Pytanie kontrolne 8.8
Stosując podstawienie x = sint oblicz całkę

W przykładzie tym obliczenie całki z iloczynu wielomianu i pierwiastka kwadratowego zostało, w wyniku podstawienia, zastąpione obliczeniem całki funkcji trygonometrycznej.
| ↔ poprzedni punkt | następny punkt ≈ |