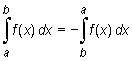Niech f będzie funkcją ciągłą, nieujemną na przedziale [a, b]. Z interpretacji geometrycznej sum całkowych wynika, że całka oznaczona, jako granica ciągu tych sum, określa pole figury płaskiej D w układzie prostokątnym kartezjańskim, ograniczonej wykresem funkcji f, osią Ox oraz prostymi x = a i x = b, nazywanej trapezem krzywoliniowym (rys. 9.4).

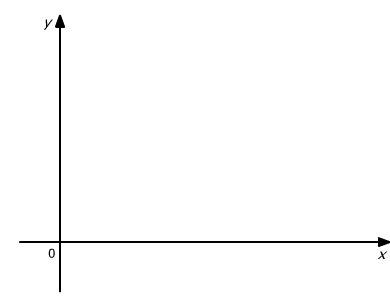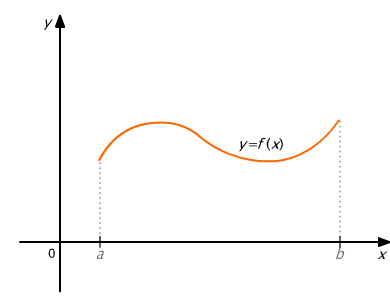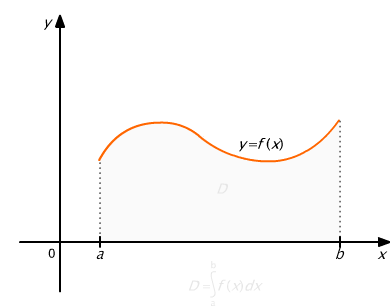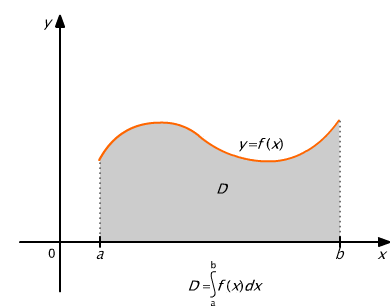
Rys. 9.4

Gdy funkcja f jest niedodatnia na przedziale [a, b] (jej wykres leży pod osią Ox), wówczas całka oznaczona podaje pole trapezu krzywoliniowego ze znakiem minus (rys. 9.5).

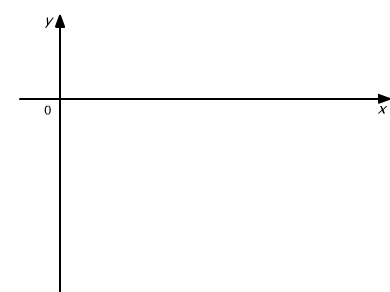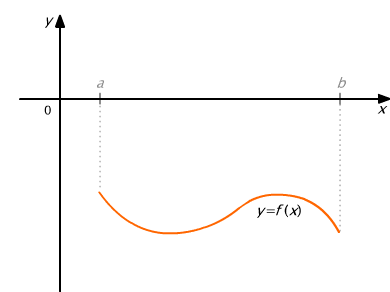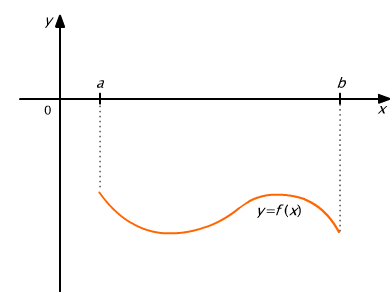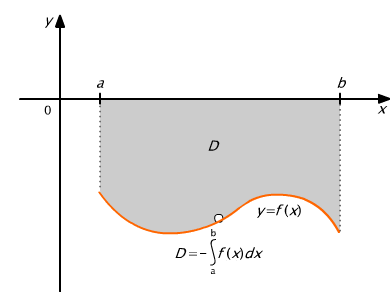
Rys. 9.5

W przypadku ogólnym całkę oznaczoną interpretujemy jako sumę algebraiczną pól leżących nad i pod osią Ox (rys. 9.6).

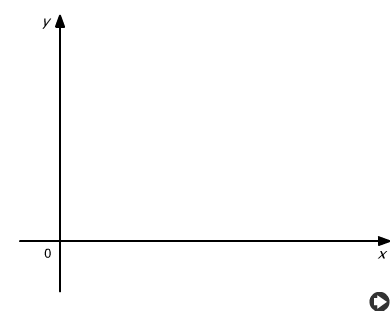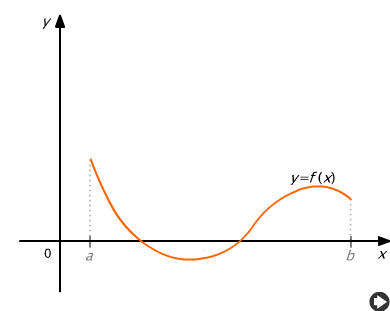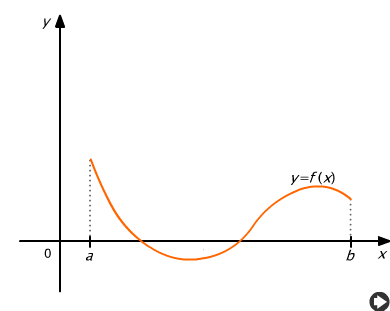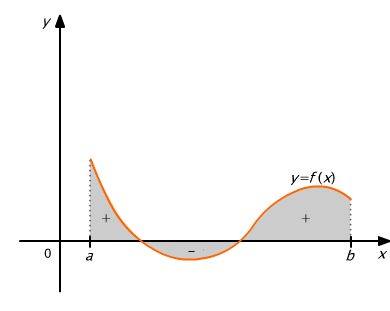
Rys. 9.6

W przyjętej definicji całki oznaczonej zakładaliśmy a < b. Jeżeli funkcja f jest całkowalna na [a, b], to dodatkowo przyjmujemy

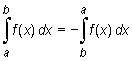oraz

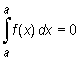Przykład

Obliczymy na podstawie definicji całkę oznaczoną funkcji stałej f(x) = c, na przedziale [a, b], tzn. całkę

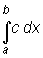
Dzielimy przedział [a, b] na n części i przez D x_k oznaczamy długość podprzedziału [x _k-1, x _k].

W przypadku funkcji stałej f(x) = c n-ta suma całkowa ma postać

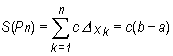
Stąd dla każdego normalnego ciągu podziałów przedziału [a, b] dostajemy

czyli

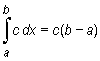
Otrzymany wynik jest zgodny z oczekiwaniami, jako że trapez krzywoliniowy miał w rozważanym przypadku kształt prostokąta o bokach c i b - a.

Z przykładu wynikają wzory

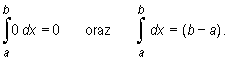Obliczenie powyższej całki okazało się bardzo proste, niemniej wyznaczanie całek oznaczonych na podstawie definicji jest w ogólnym przypadku zadaniem trudnym. W praktyce przeprowadzamy obliczenia opierając się na stosownych twierdzeniach.