
| ↔ poprzedni punkt | następny punkt ≈ |
Twierdzenie
Jeżeli funkcja f jest całkowalna na przedziale [a, b], to jest na nim ograniczona.
Uwaga
Twierdzenie odwrotne nie jest prawdziwe, tzn. nie każda funkcja ograniczona na przedziale [a, b] jest na nim całkowalna.
Przykład
Funkcja Dirichleta określona wzorem

nie jest całkowalna w żadnym przedziale [a, b], ponieważ dla ξ k wymiernych granicą ciągu sum całkowych jest długość przedziału [a, b], zaś dla ξ k niewymiernych zero, a to oznacza, że nie istnieje wspólna granica dla dowolnego wyboru argumentów funkcji f.
Warunki wystarczające całkowalności funkcji
Twierdzenie
Jeżeli funkcja f jest ciągła na przedziale [a, b], to jest na nim całkowalna.
Twierdzenie
Jeżeli funkcja f jest ograniczona na przedziale [a, b], i ma skończoną liczbę punktów nieciągłości to jest na nim całkowalna.
Uwaga
Skończona liczba punktów nieciągłości nie jest warunkiem koniecznym całkowalności funkcji.
Przykład
Funkcja określona wzorem
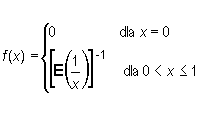
gdzie E oznacza część całkowitą liczby, jest całkowalna na przedziale [0, 1], ale w punktach x = 1/n, dla n >1, jest nieciągła (rys. 9.7).

Rys. 9.7
Twierdzenie
Jeżeli funkcja f jest monotoniczna na przedziale [a, b], to jest na nim całkowalna.
Twierdzenie (o całkowalności funkcji na podprzedziale)
Jeżeli funkcja f jest całkowalna na przedziale [a, b], to jest całkowalna na każdym podprzedziale tego przedziału.
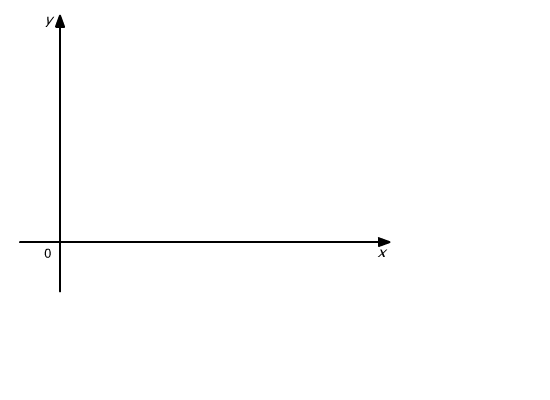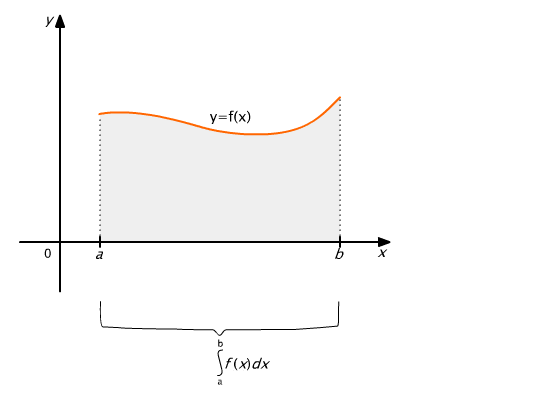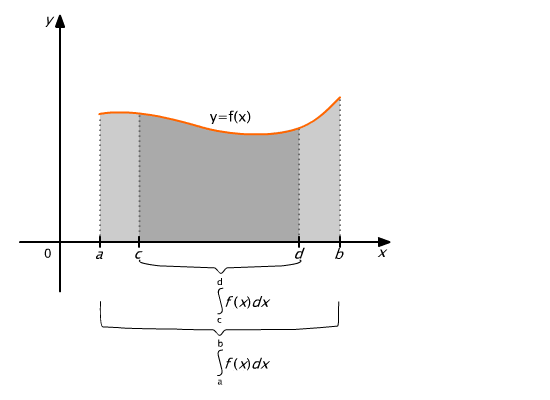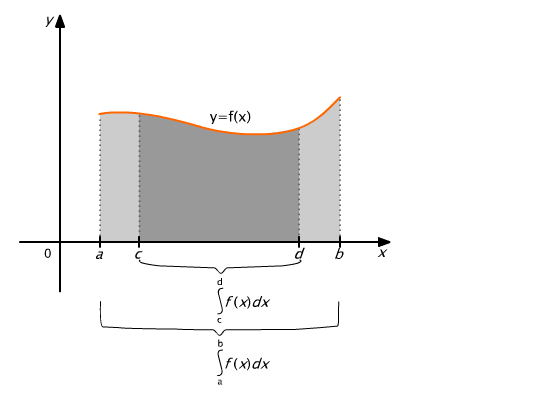
Rys. 9.8
Twierdzenie
Jeżeli funkcja f jest całkowalna na przedziale [a, b], to funkcja | f | jest też na nim całkowalna.
Uwaga
Twierdzenie odwrotne nie jest prawdziwe, co pokazuje kolejny przykład.
Przykład
Funkcja określona wzorem

nie jest całkowalna na przedziale [0, 1] (uzasadnienie analogiczne jak w przypadku funkcji Dirichleta), podczas gdy funkcja |f(x)| ≡ 1 ma na tym przedziale całkę równą 1.
Twierdzenie (o równości całek)
Jeżeli funkcje f i g różnią się w skończonej liczbie punktów przedziału [a, b] i jedna z nich jest całkowalna na tym przedziale, to druga także jest całkowalna i całki ich na przedziale [a, b] są sobie równe.
Pytanie kontrolne 9.1
Wykorzystując powyższe twierdzenie oblicz całkę
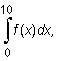
gdzie
![]()
Powyższe twierdzenia, choć gwarantują istnienie całek oznaczonych pokaźnej zbiorowości funkcji, nie dostarczają efektywnych metod ich wyznaczania.
Stosowane w praktyce metody obliczania całek opierają się na kolejnych twierdzeniach, których stosunkowo proste dowody wynikają bezpośrednio z definicji.
Twierdzenie (o liniowości całki oznaczonej)
Jeżeli funkcje f i g są całkowalne na przedziale [a, b], to funkcje f + g oraz A⋅ f, gdzie A oznacza dowolną stałą, są także całkowalne na tym przedziale, przy czym
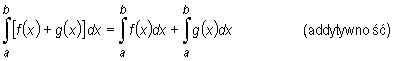 |
"całka sumy równa się sumie całek",
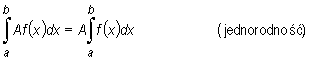 |
"stałą można wynieść/wyłączyć przed znak całki".
Twierdzenie (o zachowaniu nierówności przy całkowaniu)
Jeżeli funkcje f i g są całkowalne na przedziale [a, b] i spełniają warunek f(x) ≤ g(x), dla x∈ [a, b] , to
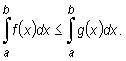 |
Twierdzenie (o wartości średniej - całkowe)
Jeżeli funkcja f jest ciągła na przedziale [a, b], to istnieje taki punkt ξ ∈ [a, b], że
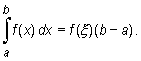 |
Dla funkcji przyjmującej wartości nieujemne, występująca w tezie równość ma następującą interpretację geometryczną. Pole trapezu krzywoliniowego wyznaczonego przez tę funkcję jest równe polu prostokąta o bokach, których długości wynoszą f(ξ) oraz b - a (rys. 9.9).

Rys. 9.9
Definicja
Wyrażenie
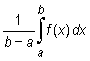 |
nazywamy wartością średnią, (lub średnią całkową) funkcji f na przedziale [a, b].
Jest to uogólnienie znanego pojęcia średniej arytmetycznej skończonej liczby składników.
Twierdzenie (o addytywności całki względem przedziału całkowania)
Jeżeli funkcja f jest całkowalna na przedziale [a, b], zaś c∈ (a, b), to
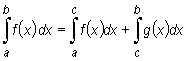 |
Twierdzenie to wykorzystujemy przy całkowaniu funkcji określonych różnymi wzorami na podprzedziałach przedziału całkowania.
Przykład
Wyznaczymy całkę oznaczoną funkcji określonej następującym wzorem
![]()
na przedziale [-1, 1].
Dzieląc przedział całkowania na podprzedziały [-1, 0] i [0, 1] otrzymujemy
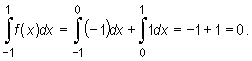
Spośród wszystkich twierdzeń szczególne miejsce zajmują tzw. podstawowe (główne) twierdzenia rachunku całkowego wiążące pojęcia całki nieoznaczonej i oznaczonej.
| ↔ poprzedni punkt | następny punkt ≈ |