| ↔ poprzedni punkt | następny punkt ≈ |
Niech f będzie funkcją całkowalną na przedziale [a, b]. Z przytoczonego wyżej twierdzenia o całkowalności funkcji na podprzedziale wynika, że całka
istnieje dla każdego x∈ [a, b]. Stąd wzór
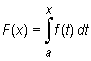 |
definiuje funkcję nazywaną funkcją górnej granicy całkowania funkcji f na przedziale [a, b] (krócej: funkcją górnej granicy całkowania).
Geometrycznie interpretuje to rys. 9.10, na którym widać, że pole określone przez całkę jest funkcją końcowej odciętej x.
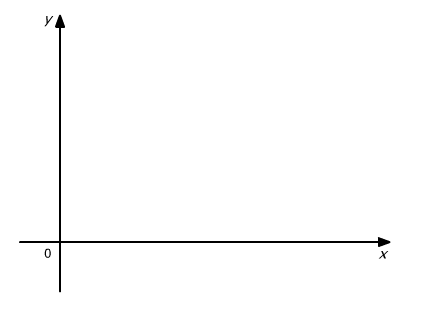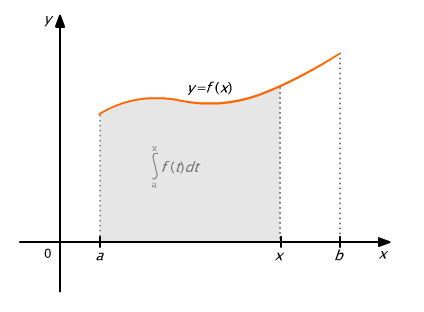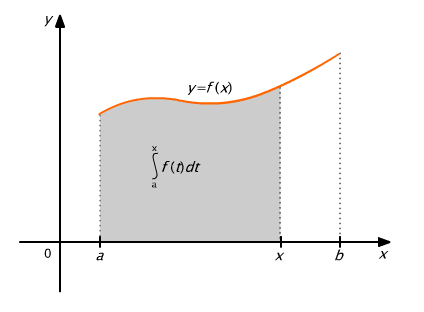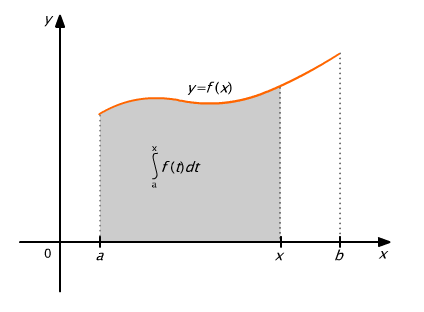
Rys. 9.10
Twierdzenie (Pierwsze główne twierdzenie rachunku całkowego)
Funkcja górnej granicy całkowania F ma następujące właściwości:
Wniosek
Jeżeli funkcja podcałkowa jest ciągła na przedziale [a, b], to równość F '(x) = f(x) zachodzi w każdym punkcie przedziału. Funkcja F jest zatem funkcją pierwotną funkcji f na tym przedziale, a wyrażenie
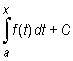 |
gdzie C oznacza stałą, jest jej całką nieoznaczoną.
Uwaga
Twierdzenie oraz wniosek pozostają prawdziwe gdy
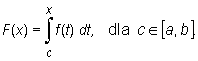 |
Powyższe twierdzenie podaje związek pomiędzy całką nieoznaczoną oraz całką oznaczoną.
Uzasadnia też podobieństwo symboli używanych do oznaczania obu typów całek. Znajomość funkcji pierwotnej (całki nieoznaczonej) umożliwia skuteczne obliczanie całki oznaczonej. Precyzuje to kolejne twierdzenie.
Twierdzenie (Drugie główne twierdzenie rachunku całkowego)
Jeżeli funkcja f jest ciągła na przedziale [a, b] oraz F jest jej dowolną funkcją pierwotną, to
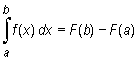 |
Występujący w tezie twierdzenia wzór nosi nazwę wzoru Newtona-Leibniza i zwykle jest zapisywany w postaci
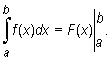 |
Wzór Newtona-Leibniza jest podstawowym narzędziem stosowanym przy obliczaniu całek oznaczonych funkcji ciągłych. W pierwszej kolejności należy wyznaczyć całkę nieoznaczoną takiej funkcji, a następnie obliczyć różnicę wartości funkcji pierwotnej na krańcach przedziału całkowania. Posługiwanie się wzorem wymaga zatem umiejętności wyznaczania całek nieoznaczonych.
Prezentowane niżej przykłady ilustrują wykorzystanie podanych twierdzeń w praktyce.
Przykłady
Obliczymy całki oznaczone
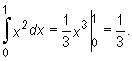
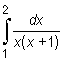
Wyznaczamy całkę nieoznaczoną
![]()
rozkładając funkcję podcałkową na ułamki proste
![]()
Z wzoru Newtona-Leibniza dostajemy
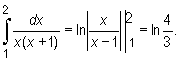
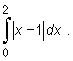
Jeżeli pod znakiem całki występuje wartość bezwzględna funkcji (ewentualnie funkcja określona różnymi wzorami na podprzedziałach), korzystnie jest podzielić przedział całkowania i skorzystać z addytywności całki względem przedziału całkowania. Stąd dostajemy
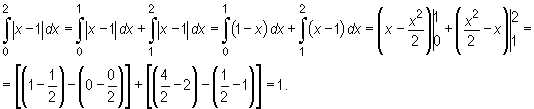
Przy obliczaniu całek oznaczonych użyteczne bywa następujące stwierdzenie.
Stwierdzenie
Jeżeli funkcja f jest całkowalna na przedziale [-a, a], gdzie a > 0, to
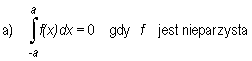 |
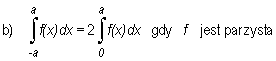 |
Geometryczne uzasadnienie wzorów przedstawia rys. 9.11.
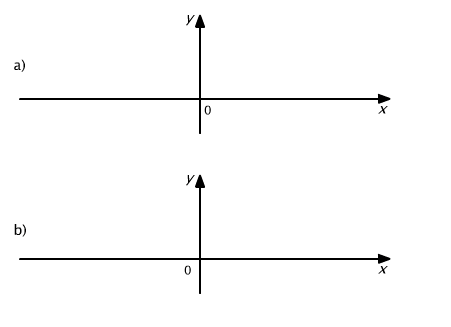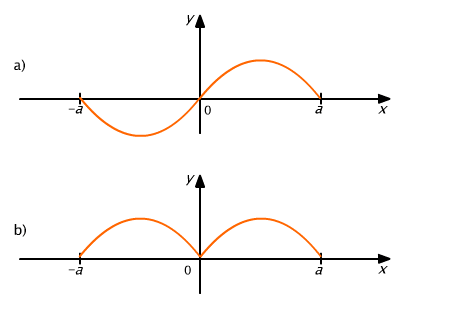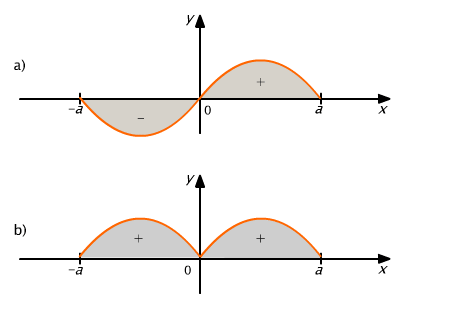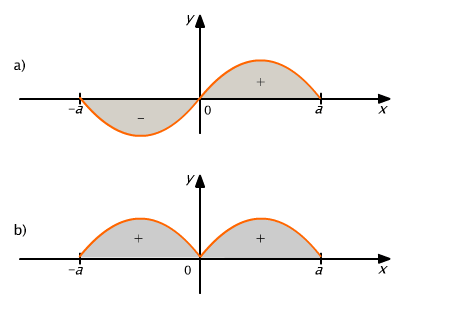
Rys. 9.11
Przykład
Bez przeprowadzania obliczeń wiadomo, że
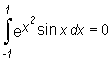
ponieważ funkcja podcałkowa jest nieparzysta.
Dla całki oznaczonej można sformułować również twierdzenia o całkowaniu przez części i przez podstawienie.
Twierdzenie (o całkowaniu przez części)
Jeżeli funkcje u i v mają na przedziale [a, b] ciągłe pochodne u' i v', to
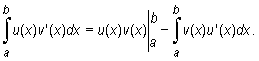 |
Przykład
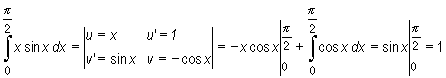
Twierdzenie (o całkowaniu przez podstawienie)
Jeżeli funkcja f jest całkowalna na przedziale [a, b], zaś funkcja g ma ciągłą pochodną na przedziale [a , b ] i przekształca go na przedziale [a, b], a ponadto g(a ) = a oraz g(b ) = b, to zachodzi wzór
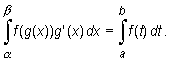 |
Przykład
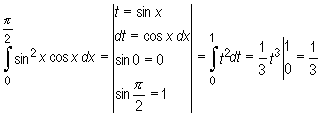
Uwaga
Zazwyczaj wygodniej jest realizować obliczenia wyznaczając całkę nieoznaczoną funkcji, a następnie stosując wzór Newtona-Leibniza.
| ↔ poprzedni punkt | następny punkt ≈ |