Definicja
Jeżeli funkcja f jest określona na przedziale [a, ∞ ), całkowalna na każdym przedziale [a, T] (T > a), i istnieje granica skończona
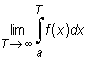 |
to granicę tę nazywamy całką niewłaściwą I rodzaju funkcji f na przedziale [a, ∞) i oznaczamy
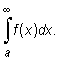 |
| ↔ poprzedni punkt |
Definiując całkę oznaczoną Riemanna zakładaliśmy, że przedział całkowania jest skończony, zaś funkcja podcałkowa jest na nim ograniczona. Zajmiemy się obecnie rozszerzeniem pojęcia całki na przypadki, gdy warunki te nie są spełnione.
Definicja
Jeżeli funkcja f jest określona na przedziale [a, ∞ ), całkowalna na każdym przedziale [a, T] (T > a), i istnieje granica skończona
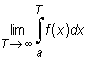 |
to granicę tę nazywamy całką niewłaściwą I rodzaju funkcji f na przedziale [a, ∞) i oznaczamy
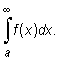 |
Czyli
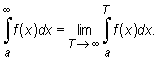 |
Analogicznie definiujemy całkę niewłaściwą I rodzaju funkcji f na przedziale (-∞, a], tzn.
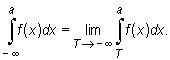 |
oraz całkę niewłaściwą I rodzaju funkcji f na przedziale (-∞, ∞ )
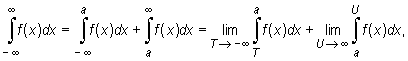 |
gdzie a jest dowolną liczbą rzeczywistą.
Jeśli granica występująca w definicji całki niewłaściwej nie istnieje, lub jest nieskończona to mówimy, że całka jest rozbieżna. W przeciwnym wypadku mówimy, że jest zbieżna.
Geometrycznie całkę niewłaściwą pierwszego rodzaju interpretujemy jako pole figury płaskiej rozciągającej się nieograniczenie wzdłuż osi Ox.
Przykłady
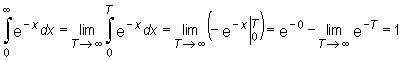
Całka ta podaje pole zacienionego obszaru z rys. 9.12
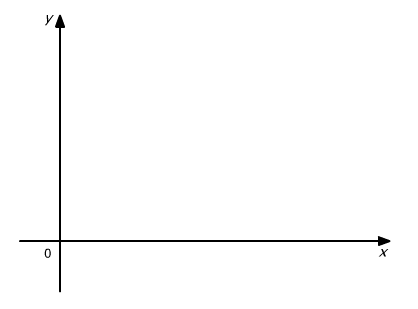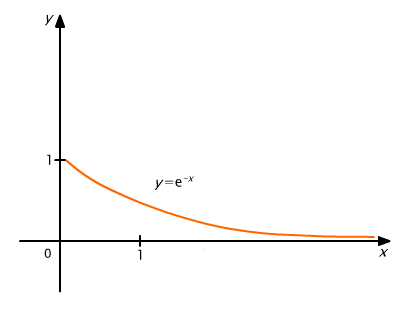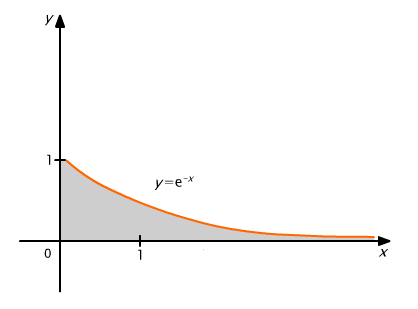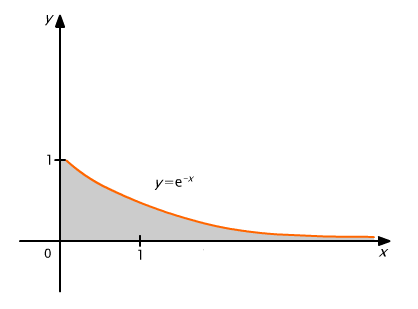
Rys. 9.12
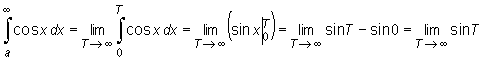
Ponieważ ostatnia granica nie istnieje całka jest rozbieżna.
Niech funkcja f będzie określona na przedziale [a, b), całkowalna w każdym przedziale [a, b - ε ], 0 < ε < b - a oraz nieograniczona w sąsiedztwie punktu b.
Definicja
Jeżeli istnieje granica skończona
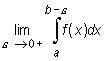 |
to granicę tę nazywamy całką niewłaściwą II rodzaju funkcji f na przedziale [a, b) i oznaczamy
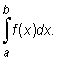 |
Czyli
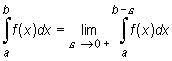 |
W analogiczny sposób definiujemy całkę całką niewłaściwą II rodzaju funkcji f na przedziale (a,b], tzn.
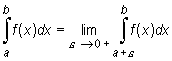 |
Jeżeli funkcja jest nieograniczona w otoczeniu punktu c należącego do wnętrza przedziału [a, b], wówczas całkę niewłaściwą określamy następująco
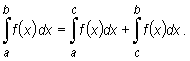 |
o ile obie całki po prawej stronie równości istnieją, w myśl wcześniej podanych określeń.
Przykład
Obliczymy całkę niewłaściwą II rodzaju
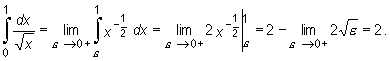
Oznacza to, że prezentowany na rys. 9.13 obszar, ograniczony osią Ox, prostą x = 0 (czyli osią Oy), prostą x = 1 i wykresem funkcji f(x) = x -1/2 ma pole równe 2.
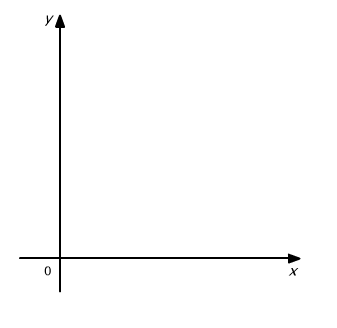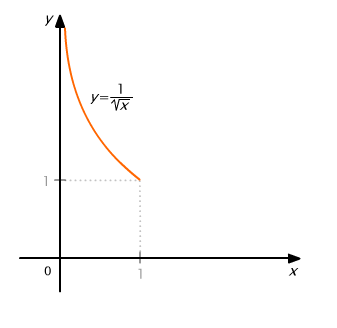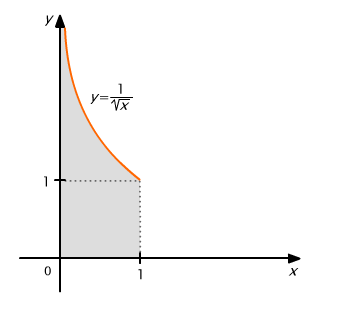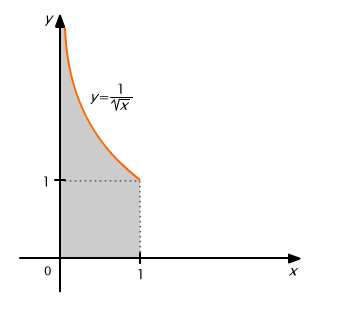
Rys. 9.13
Kończąc omawianie metod całkowania odnotujmy kilka uwag.
Uwagi
podczas gdy całka nieoznaczona tej funkcji nie da się wyrazić za pomocą funkcji elementarnych.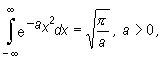
| ↔ poprzedni punkt |