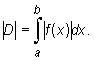
| następny punkt ≈ |
Zgodnie z interpretacją geometryczną całki oznaczonej obliczenie pola powierzchni trapezu krzywoliniowego dla funkcji nieujemnej jest równoważne z wyznaczeniem całki oznaczonej tej funkcji. Ponieważ dla funkcji niedodatniej całka podaje pole figury ze znakiem minus, ogólny wzór na pole figury płaskiej przyjmuje postać
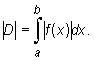 |
W praktyce rachunkowej oznacza to oddzielne wyznaczanie pól nad i pod osią Ox, a następnie ich zsumowanie.
Przykład
Obliczymy pole figury ograniczonej osią Ox , prostymi x = 0, x = 3π/2 oraz wykresem funkcji cosinus (rys. 10.1).
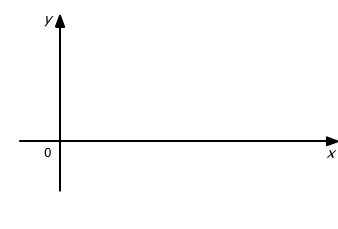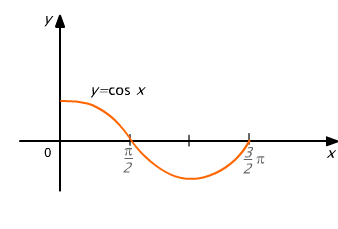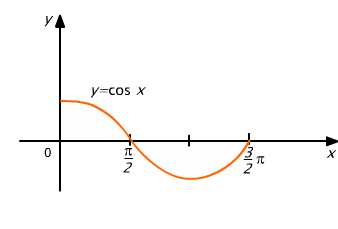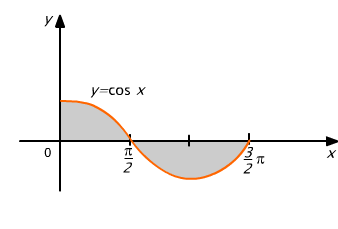
Rys. 10.1
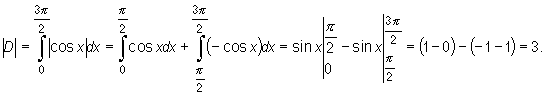
Uwaga
Przedział [a, b] może być nieograniczony.
Przykładem jest poniższe zadanie.
Pytanie kontrolne 10.1
Oblicz pole figury ograniczonej osią Ox oraz krzywą
![]()
Wzór pozwalający obliczać pole powierzchni można w naturalny sposób uogólnić na przypadek pola figury (zwanej obszarem normalnym) definiowanej przez dwie funkcje (rys. 10.3).

Rys. 10.3
Twierdzenie
Jeżeli funkcje f i g są ciągłe na przedziale [a, b] i spełniają na nim warunek g(x) ≤ f(x), to pole obszaru D, ograniczonego krzywymi y = f(x), y = g(x) oraz prostymi x = a i x = b, jest równe
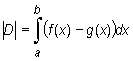 |
(zauważmy, że dla funkcji g(x) ≡ 0 dostajemy wcześniej stosowany wzór).
Zobacz dowódPrzykład
Obliczymy pole obszaru ograniczonego wykresami funkcji
![]()
Aby wyznaczyć granice całkowania znajdujemy punkty przecięcia się krzywych rozwiązując układ równań
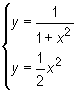
Dostajemy
![]()
Zatem szukane pole D jest wyznaczone przez funkcje f i g na przedziale [-1, 1], na którym zachodzi nierówność f(x) ≥ g(x) (rys. 10.4).
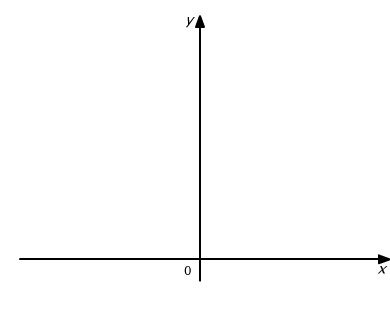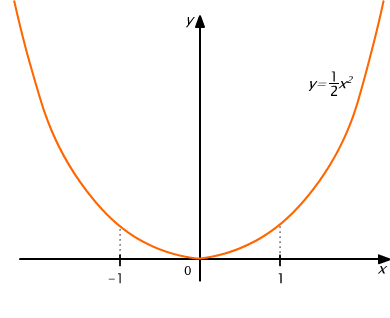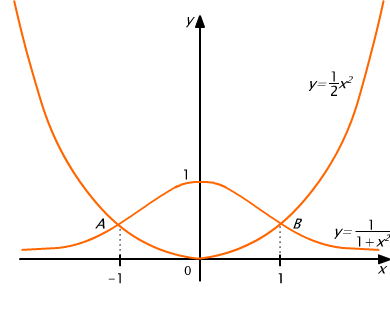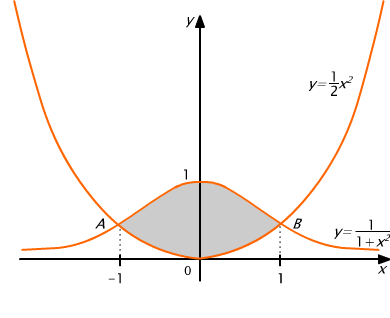
Rys. 10.4
Obliczamy szukane pole wykorzystując jego symetrię względem osi Oy (parzystość funkcji podcałkowej)
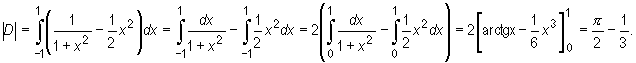
Pytanie kontrolne 10.2
Oblicz pole figury płaskiej ograniczonej wykresami funkcji
![]()
| następny punkt ≈ |