| ↔ poprzedni punkt | następny punkt ≈ |
Pojecie całki oznaczonej pojawia się w opisach modeli fizycznych bardzo często. W niniejszym wykładzie ograniczymy się do zaprezentowania trzech prostych przykładów.
Droga w ruchu zmiennym
Niech punkt materialny porusza się ruchem prostoliniowym ze zmienną w czasie prędkością v. Wówczas droga przebyta przez ten punkt w przedziale czasu [t1, t2] jest dana wzorem
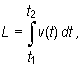 |
gdzie v(t) jest prędkością chwilową.
Przykład
Przez 10s, od chwili startu, pojazd poruszał się ruchem jednostajnie przyspieszonym, z przyspieszeniem a = 2m/s2. Następnie, przez minutę poruszał się ze stałą prędkością. Po tym czasie rozpoczął hamowanie z opóźnieniem a = - 1m/s2. Obliczymy drogę jaką przebył samochód od startu do zatrzymania.
Wykorzystując wzór na prędkość chwilową w ruchu jednostajnie przyspieszonym v(t) = v0 +a(t - t0), gdzie v0 oznacza prędkość początkową prędkość chwili t0, wyznaczamy prędkość chwilową z jaką poruszał się pojazd
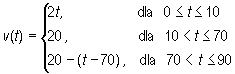
Stąd przebyta droga
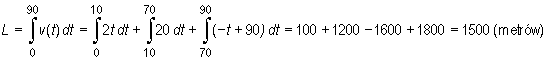 .
.
Praca wykonywana przez zmienną siłę
Jeżeli równolegle do osi Ox działa zmienna siła F, to praca wykonana przez tę siłę na drodze od punktu a do punktu b wyraża się wzorem
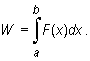 |
Przykład
Obliczymy pracę jaką należy wykonać, aby ciało o masie m podnieść z powierzchni Ziemi na wysokość h.
Na wysokości x nad powierzchnią Ziemi odległość między środkami mas wynosi R + x. Siła przyciągania wzajemnego (grawitacji) wynosi zatem
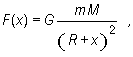
gdzie M - masa Ziemi, G - stała grawitacji.
Stąd praca
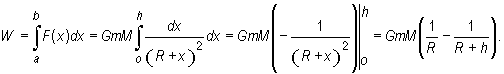
Energia pobrana ze źródła prądu zmiennego
Jeżeli u oraz i oznaczają odpowiednio wartości chwilowe napięcia i natężenia prądu zmiennego, to całkowitą energię pobraną w czasie t ze źródła tego prądu obliczamy ze wzoru
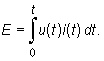 |
Przykład
Obliczymy energię pobieraną przez odbiornik o oporze czynnym R, podłączonym do źródła prądu zmiennego o napięciu chwilowym u(t) = Usinω t, gdzie ω jest pulsacją prądu (ω = 2π /T, T - okres zmian), w ciągu 200 okresów, tzn. dla t = 200T.
Z prawa Ohma chwilowa wartość natężenia prądu wynosi
![]()
Zatem
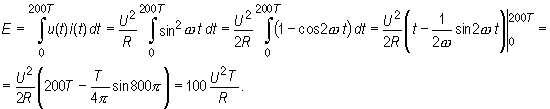
Pytanie kontrolne 10.6
W obwodzie, przedstawionym na rys. 10.11, kondensator o pojemności C został naładowany do napięcia U. Oblicz energię straconą na oporze R przy rozładowywaniu kondensatora po zamknięciu obwodu, jeżeli wiadomo, że chwilowy prąd wyładowania kondensatora określa wzór
![]()
gdzie t jest czasem mierzonym od chwili zamknięcia obwodu, zaś τ = RC stałą czasu.
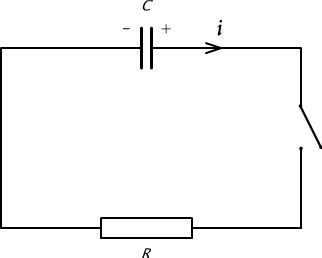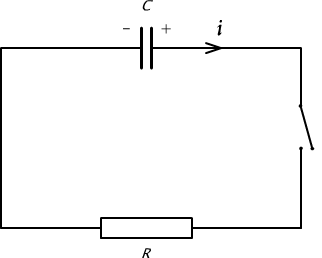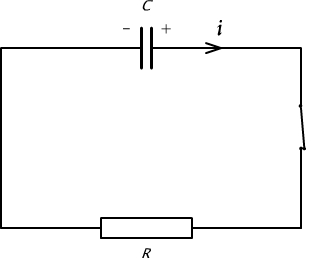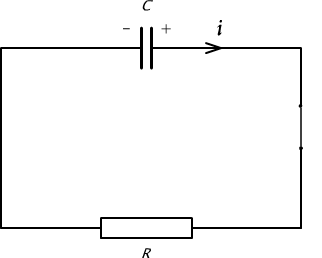
Rys. 10.11
Zobacz odpowiedź| ↔ poprzedni punkt | następny punkt ≈ |