Definicja (granica ciągu punktów przestrzeni R^m)

Mówimy, że ciąg (A⁽ⁿ⁾) punktów przestrzeni R^m jest zbieżny do punktu A⁽⁰⁾∈ R^m

oraz piszemy jeśli

Można pokazać, że

wtedy i tylko wtedy gdy ciąg pierwszych współrzędnych punktów A⁽ⁿ⁾ jest zbieżny do pierwszej współrzędnej punktu A⁽⁰⁾, ciąg drugich współrzędnych punktów A⁽ⁿ⁾ jest zbieżny do drugiej współrzędnej punktu A⁽⁰⁾,..., ciąg m-tych współrzędnych punktów A⁽ⁿ⁾ jest zbieżny do m-tej współrzędnej punktu A⁽⁰⁾.

Definicja (definicja Heinego granicy funkcji)

Niech f : D → R, D ⊂ R^m, m ≥ 2, A⁽⁰⁾∈ R^m oraz niech funkcja f będzie określona przynajmniej w pewnym sąsiedztwie punktu A⁽⁰⁾. Powiemy, że funkcja f ma w punkcie A⁽⁰⁾ granicę g, co zapisujemy , jeśli dla każdego ciągu (A⁽ⁿ⁾) punktów zbioru D różnych od punktu A⁽⁰⁾ takiego, że mamy

• Gdy A⁽⁰⁾ = (a₁, a₂,..., a_m), to zamiast pisać

często piszemy

• Gdy n = 2, A⁽⁰⁾= (a, b), to zamiast

piszemy też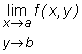

. Analogiczne oznaczenia stosujemy też dla funkcji trzech zmiennych.

• Gdy g jest liczbą, to mówimy o granicy właściwej. Gdy g = ∞ lub g = − ∞, to mówimy o granicy niewłaściwej.

Definicja

Niech f : D → R, D ⊂ R^m. Powiemy, że funkcja f jest ciągła w punkcie A⁽⁰⁾, jeśli istnieje otoczenie punktu A⁽⁰⁾ zawarte w zbiorze D oraz

Definicja

Niech f : D → R, D ⊂ R^m. Powiemy, że funkcja f jest ciągła na (w) zbiorze D, jeśli f jest ciągła w każdym punkcie zbioru D.

Zwrot 'funkcja f jest ciągła' oznacza, że f jest ciągła w całej swojej dziedzinie.

Większość funkcji wielu zmiennych, z którymi spotyka się inżynier to są funkcji ciągłe co wynika z następującego twierdzenia:

Twierdzenie

Każda funkcja wielomianowa f : R^m → R czyli funkcja postaci jest ciągła.
Jeżeli f : D → R, D ⊂ R^m jest ciągła , g : f(D) → R jest ciągła, to złożenie funkcji g oraz f, : D → R też jest funkcją ciągłą.
Jeżeli f : D → R, g : D → R, D ⊂ R^m są funkcjami ciągłymi, to ciągłe są również
• każda kombinacja liniowa funkcji f i g,

• iloczyn f⋅ g

• iloraz f/ g (na zbiorze D₁ = {A∈ D : g(A) ≠ 0}
Jeśli funkcje f₁, f₂, ..., f_m : U → R, U ⊂ Rⁿ, są ciągłe, funkcja g : V → R, V ⊂ R^m oraz (f₁(x), f₂(x), ..., f_m(x))∈ V dla każdego x∈ U, to funkcja złożona określona wzorem g(f₁(x), f₂(x), ..., f_m(x)) jest ciągła na U.

są ciągłe w swoich dziedzinach. Pierwsza jako funkcja wielomianowa na R³, druga jako iloraz funkcji wielomianowych na R² a ciągłość ostatniej wynika z ciągłości funkcji g(x,y) oraz z punktu (2) poprzedniego twierdzenia.

Twierdzenie (o zachowywaniu znaku)

Jeśli funkcja f : D → R, D ⊂ R^m jest ciągła w punkcie A⁽⁰⁾∈ D oraz f(A⁽⁰⁾) > 0, to istnieje liczba ε > 0 taka, że spełniony jest warunek

Oczywiście twierdzenie to pozostaje prawdziwe, gdy symbol > zastąpimy w nim przez <.

Twierdzenie (Weierstrassa)

Jeżeli funkcja f : D → R jest ciągła oraz zbiór D ⊂ R^m jest niepusty, domknięty i ograniczony, to w zbiorze tym istnieją punkty P₁, P₂ takie, że dla dowolnego punktu P zbioru D zachodzą nierówności:

Oznacza to, że funkcja ciągła na niepustym, domkniętym i ograniczonym podzbiorze D przestrzeni R^m jest na nim ograniczona i co więcej przyjmuje kres dolny f(P₁) i kres górny f(P₂) swoich wartości.