3. POCHODNE CZĄSTKOWE PIERWSZEGO RZĘDU
Definicja
Niech f : D →
R, D ⊂
Rm , A∈
IntD, A =
(
a1, ..., an)
. Jeżeli istnieje granica właściwa (funkcji jednej zmiennej h)
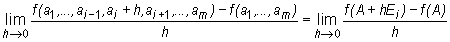 ,
,
(gdzie Ei =
(0, ...,1, ..., 0) jest i-tym wektorem bazy kanonicznej przestrzeni Rn),
to granicę tę nazywamy pochodną cząstkową pierwszego rzędu funkcji f względem zmiennej xi w punkcie A i oznaczamy jednym z symboli: 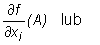
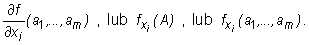
Symbolem 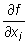 (i = 1, ..., m) oznaczamy funkcję określoną na zbiorze
(i = 1, ..., m) oznaczamy funkcję określoną na zbiorze 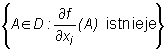 przyporządkowującą punktowi A liczbę
przyporządkowującą punktowi A liczbę 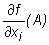 .
.
Funkcje 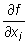 , i =
1, ..., m nazywamy pochodnymi cząstkowymi pierwszego rzędu funkcji f.
, i =
1, ..., m nazywamy pochodnymi cząstkowymi pierwszego rzędu funkcji f.
Dla m = 2 zamiast pisać  piszemy
piszemy 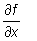 lub fx; zamiast
lub fx; zamiast 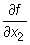 piszemy
piszemy 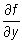 lub fy. Podobnie postępujemy gdy m = 3 z tym, że zamiast
lub fy. Podobnie postępujemy gdy m = 3 z tym, że zamiast 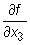 piszemy
piszemy 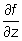 lub fz.
lub fz.
Zatem
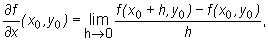
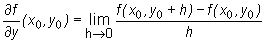
i dla funkcji trzech zmiennych
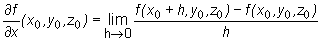
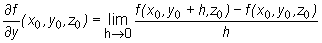
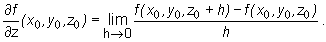
Przykład
Niech f(x, y) = x2 + 2xy2 + cosx - 2y . Wykorzystując definicję obliczymy
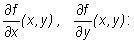
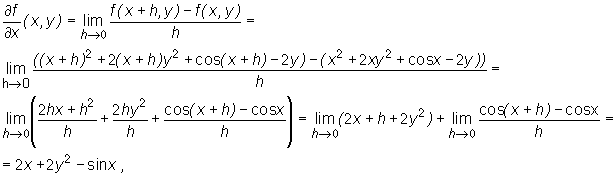
ponieważ
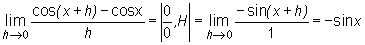 ;
;
podobnie
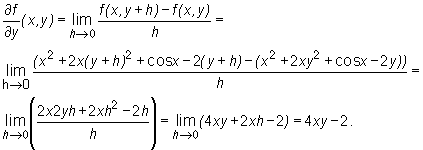
Uwaga
Obliczając 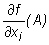 traktujemy wszystkie zmienne xj dla j ≠
i jako stałe i wyznaczamy pochodną w punkcie ai funkcji f traktowanej jako funkcję jednej zmiennej xi.
traktujemy wszystkie zmienne xj dla j ≠
i jako stałe i wyznaczamy pochodną w punkcie ai funkcji f traktowanej jako funkcję jednej zmiennej xi.
Dokładniej: 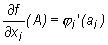 , gdzie φ
i(x) = f(a1, ..., ai-1, x, ai+1, ...am).
, gdzie φ
i(x) = f(a1, ..., ai-1, x, ai+1, ...am).
Wynika stąd, że licząc pochodne cząstkowe możemy stosować wszystkie znane reguły liczenia pochodnej funkcji jednej zmiennej, w szczególności wzory na pochodną sumy, iloczynu, ilorazu, iloczynu funkcji przez stałą.
Przykład
•
Niech f(x, y) = x2 + 2y2x + sinx - 3x3y.
Obliczając  traktujemy y jako stałą (zatem 2y2, 3y są stałymi), zaś f jako funkcję zmiennej x) i otrzymujemy:
traktujemy y jako stałą (zatem 2y2, 3y są stałymi), zaś f jako funkcję zmiennej x) i otrzymujemy:
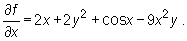
Licząc  traktujemy x, a więc również x2, 2x, sinx, 3x3, jako stałe, zaś f jako funkcję zmiennej y, a to daje
traktujemy x, a więc również x2, 2x, sinx, 3x3, jako stałe, zaś f jako funkcję zmiennej y, a to daje 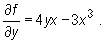
•
Obliczmy pochodne cząstkowe funkcji 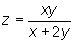 w punkcie A=(1,2).
w punkcie A=(1,2).
Traktując z jako funkcję zmiennej x i stosując odpowiednie wzory na pochodną funkcji jednej zmiennej dostajemy:
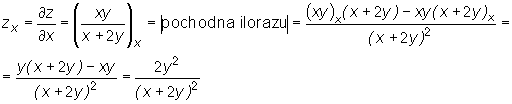 .
.
Analogicznie:
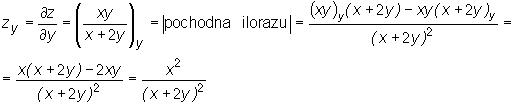 .
.
Zatem

•
Obliczmy pochodne cząstkowe pierwszego rzędu funkcji trzech zmiennych 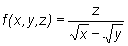 .
.
Postępując podobnie jak w poprzednich przykładach dostajemy:
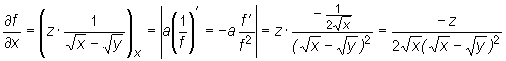
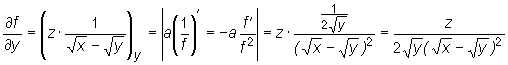
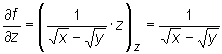 .
.
Korzystaliśmy z tego, że przy liczeniu pierwszej pochodnej z oraz 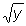 traktujemy jako stałe, podobnie przy liczeniu drugiej pochodnej z oraz
traktujemy jako stałe, podobnie przy liczeniu drugiej pochodnej z oraz 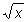 traktujemy jako stałe a przy liczeniu trzeciej pochodnej
traktujemy jako stałe a przy liczeniu trzeciej pochodnej 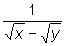 traktujemy jako stałą.
traktujemy jako stałą.
•
Obliczmy jeszcze pochodne cząstkowe pierwszego rzędu funkcji
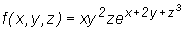 .
.
Mamy
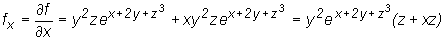
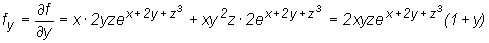
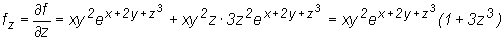
W tym przykładzie licząc każdą z pochodnych cząstkowych korzystaliśmy z wzoru na pochodną iloczynu funkcji.
•
Niech z(x, y) = x2y. Obliczamy 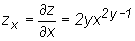 - tu funkcję z(x, y) rozpatrujemy jako funkcję potęgową xa
zmiennej x, gdzie a
=
2y;
- tu funkcję z(x, y) rozpatrujemy jako funkcję potęgową xa
zmiennej x, gdzie a
=
2y;
Obliczając zy traktujemy z(x, y) jako funkcję zmiennej y, a jest to funkcja postaci aφ
(y), gdzie φ
(y) = 2y, a = x. Zatem
 .
.
![]() ,
,![]()
![]()
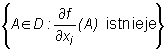 przyporządkowującą punktowi A liczbę
przyporządkowującą punktowi A liczbę 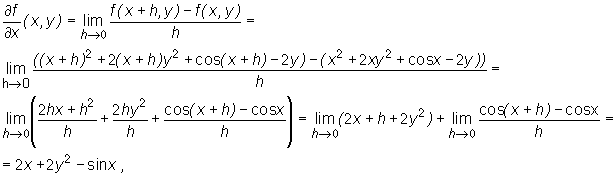
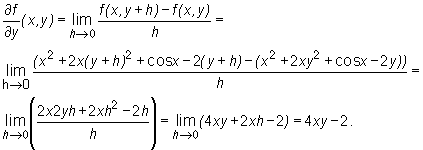
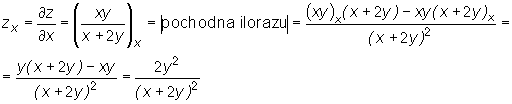 .
.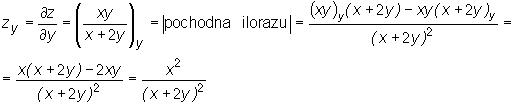 .
.
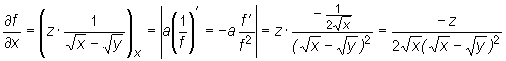
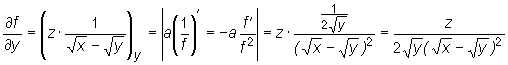
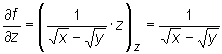 .
.