Digital image representation

Image, similarly to all kind of information in computer, must be represented in digital form. In this lecture a method of image representation in digital form is explained. Problems associated with using such representation are discussed.

In surrounding world we observe continuous images consisting of infinite number of points, wherein each point may be represented by infinite number of values. Each attempt to represent such images in digital form means necessity to limit both number of modelled points by image sampling and number of values assigned to particular points by quantization of real range of values.

Image sampling process may be demonstratively explained as follows. Let us imagine that we put rectangular mesh (Fig. II.1a) on a photo (we accept simplifying assumption that good quality photo reflects the real image). Each node of mesh corresponds to single image sample. A set of such specified samples is some approximation of image, the better the bigger is the number of samples.

Each image sample has some colour Bpr. We may assign the closest colour Bpiks taken from admissible set of colours. The cardinality of this set is defined by the length of binary word that represents colour in graphic system. Digital representation of image sample is referred to as pixel.

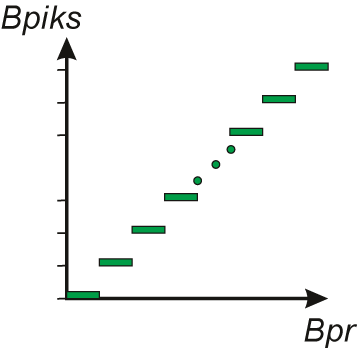
Fig. II.1. Illustration of: a) image sampling process b) sample colour quantization process

As far as the conversion of real images to digital form requires image sampling and quantisation of samples, the reverse conversion does not require any operations. It follows the observation of displayed image by human user. The fact is used that human visual system allows perception of discrete information, such as digital image as continuous information (provided good enough digital image visualisation)

Beside the image representation described above, where the samples are identified with mesh nodes, the representation where samples are identified with mesh eyelets is also possible. Then the colour averaged over the whole surface of the mesh eyelet is assigned to the sample.

Described methods of digital representation of real image are reflected in two models of image representation: point and surface. Both models are shown in Fig. II.2. It is worth noting that both models are approximate method of representation of displayed pixels, because in reality pixels are nor infinitely small (as in point model) neither do not fill the screen surface in continuous way (as in surface model). In practice both models are used dependent on convenience. Let us pay attention to the way of defining pixel coordinates in both methods. In point method they are row number and column number describing the mesh node where the pixel is placed. In surface model the are coordinates of the centre of mesh eyelet - that means shift of the coordinates of particular pixels by ½ of mesh pitch in comparison to point model coordinates.

Fig. II.2 Two equivalent pixel representations: a) point b) surface

Let us notice that operations of sampling and quantifying of real images are performed by digital cameras, where the real images are fixed in digital images form. In computer graphics digital images and specifically particular pixel from these images are generated using appropriate computational methods.

If we associate rectangular coordinate system $x,y$, with rectangular mesh of digital image pixels then we may describe the placement of each pixel p giving its coordinates $x_p,y_p$. Finally the image is represented by rectangular matrix $m×n$ pixels, where m and n represents the number of pixels in horizontal and vertical direction respectively. These numbers define so called pixel resolution of image, for example 1920 x 1080. Such defined resolution is independent on physical size of the image - it specifies the number of pixels devoted to image representation. In practice we may found different pixel resolutions. Nowadays the most frequently used pixel resolution has the horizontal resolution to vertical resolution ratio equal to 16/9. Previously this ratio was equal to 4/3.

Next to image pixel resolution there also exists linear image resolution (ppi), which define the number of pixels displayed on the one inch line. This value is relevant to define the size of the image reproduced on different devices. In printers we may find similar parameter (dpi) defining the number of printable dots/points on the line of 1 inch length.

Image represented as matrix of pixels frequently is named pixel map. In practice we may find term bit map, or just bitmap, no matter how many bits is used for pixel representation.

In order to store image in the form of pixel map we need adequate memory capacity. For example if the image has pixel resolution 1920 x 1080 and the colour of single pixel is represented on 24 bits we need 1920 x 1080 x 24 bits in memory i.e. approximately 49.77 Mb or 6.22 MB.

Image pixel resolution is not a fixed feature. The image may be presented with different resolution depending on needs or parameters of sampling devices, storing and displaying devices. Obviously the greater is image resolution the better is the approximation of real image In Fig. II.3 the same image with different pixel resolution is presented.

Fig. II.3. The image presented with different pixel resolutions

Similarly to image pixel resolution the number of bits used to represent the colour of single pixel is not a fixed feature of the image. Using greater number of bits we get better approximation of real colour. In Fig. II.4 the same image with different number of bits representing the colour of single pixel is presented. In both cases pixel resolution of the image is the same.

Fig. II.4. Image displayed with different number of bits per pixel

But the excessive increase the number of pixels representing pixel colour is meaningless due to limited abilities of human colour perception. It is accepted that for photo realistic images it is sufficient to use 8 bit to code luminance information or intensity of each primary colour R, G and B. Sometime it is necessary to increase this number to 10 or 12 bits.

In computer practice we use screens with different pixel resolutions. As far as time flows and technology is developing these resolutions become greater - long time ago it was 320 x 240, now typical value is 1920 x 1080. The question arises whether exist any limits for increase resolution of displays. It seems that meaningful limitations come from limited ability of human visual system to distinguish minute details. The rule of thumb tells that a man can distinguish the details seen at the angle of 1 arc minute. Assuming that typical distance between the observer and the screen is approximately equal to 0.5 m it is possibly to calculate the reasonable resolution with regard to perception of small details.

Example

Observer watches the image of 30 cm width from the 50 cm distance. Assuming that observer is capable to distinguish the detail seen at 1 arcmin (1’) angle calculate approximate number of horizontal pixels distinguishable by observer.

Using the above figure we may write down that $\tan α/2=0,3$. Hence $α/2≅17°$ and $α≅34°$. At assumed visual acuity and remembering that, $1°=60’$ we get sought result

$34∗60=2040$ pixels

Sometimes it is necessary to change image resolution. In general case the calculations of resolution change may be done as follows. Lets assume the situation presented in Fig. II.5a. The new rectangular mesh (marked by bold lines) of target resolution is imposed over existing rectangular mesh. The pitch of both meshes is known. The part of Fig. II.5a marked by a circle is shown enlarged in Fig. II.5b.

Fig. II.5. Change of resolution in point representation of pixels

Problem relies on finding the value of pixel N from new mesh if we know the value (intensity) of A,B,C,D pixels in image with initial resolution. We assume known value α and β defining pixel N placement in ABCD square.

Let us consider A and B pixels. Using interpolation method we may find the value of intensity in auxiliary point P1 lying on AB line segment and dividing this segment by the ratio α : (1-α), as

P1 = α B + (1 - α) A.

In the same way we may find the intensity value for P2 point lying between C and D pixels as

P2 = α D + (1 - α) C.

Finally knowing the intensity values in points P1 and P2, using once more interpolation method we may find the intensity value of pixel N as

N = β P2 + (1 - β) P1.